[ENGN2211 Home]

Circuit Analysis

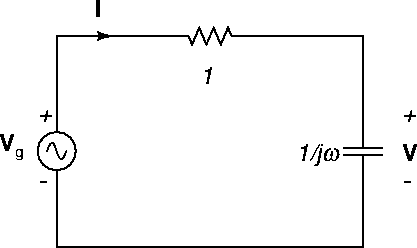
Let's analyse the steady state AC response of the circuit of Figure 33 using phasors. The phasor circuit is shown in Figure 37. Here, ${\mathbf V}_g = 5\angle 0$ V.

  

Figure 37: RC phasor circuit showing AC impedances.

By KVL and Ohm's law, we have

$${\mathbf V}_g = {\mathbf I} (1+\frac{1}{j2}) ,$$

and so

$${\mathbf I} = \frac{{\mathbf V}_g}{1+\frac{1}{j2}} = \frac{j2 \times 5\angle 0}{1+j2}$$

or

$${\mathbf I} = 4+j2 = 2\sqrt{5} \angle 26.6^\circ \ {\rm A} .$$

Then by Ohm's law,

$${\mathbf V} = {\mathbf I} \frac{1}{j2} = 1-j2 \ {\rm V} ,$$

or

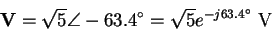$${\mathbf V} = \sqrt{5}\angle -63.4^\circ = \sqrt{5}e^{-j63.4^\circ} \ {\rm V}$$ (47)

in agreement with (46) and (45).

We obtain the real voltage by

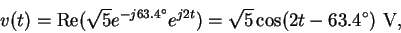$$v(t) = {\rm Re} ( \sqrt{5}e^{-j63.4^\circ} e^{j2t} ) = \sqrt{5} \cos(2t -63.4^\circ) \ {\rm V} ,$$ (48)

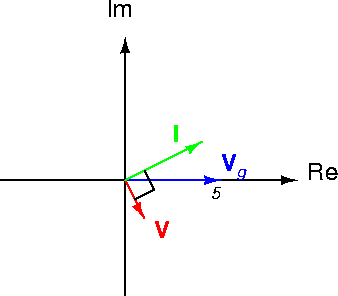
in agreement with (42). The phasor diagram for this problem is shown in Figure 38.

  

Figure 38: RC phasor diagram.

[ENGN2211 Home]