[ENGN2211 Home]

   
Impedances

Ohm's law and impedances can be obtained from the s-domain impedances of Table 2 in §3.2.4 on setting $s=j\omega$. AC impedances are shown in Table 3, and Ohm's law reads

V = Z I

where Z is the complex AC impedance, and V, I are voltage and current phasors.

 

Table 3: AC impedances.

Resistor	Z =R
Capacitor	$${{\mathbf Z} =\frac{1}{j\omega C}}$$
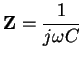Inductor	${\mathbf Z} = j\omega L$

 

Ohm's law indicates the following phase relationships:

• For resistors, current and voltage are in phase.
• For capacitors, current leads voltage by $90^\circ$.  
• For inductors, current lags voltage by $90^\circ$.  

This is illustrated in Figure 36.

  

Figure 36: Phasor diagram indicating current-voltage phase relationships for resistors, capacitors, and inductors.

In general, impedances are complex numbers, and so we write

Z = R + j X

where

$R = {\rm Re}({\mathbf Z})$ is the resistive component, and

$X = {\rm Im}({\mathbf Z})$ is the reactive component, called the reactance.  

The admittance   is the reciprocal of impedance:

$${\mathbf Y} = \frac{1}{{\mathbf Z}}$$

and we write

Y = G + j B

where

$G = {\rm Re}({\mathbf Y})$ is the conductance, and  

$B = {\rm Im}({\mathbf Y})$ is the susceptance.  

[ENGN2211 Home]