[ENGN2211 Home]

JFET Biasing

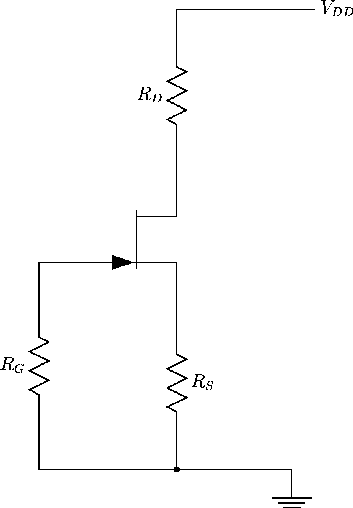
Consider an n-type JFET. It requires V_GS to be negative. Perhaps the simplest way to achieve this is via the self-bias   circuit of Figure 132.

  

Figure 132: n-channel JFET self bias.

The gate is tied to ground (0 V) via a resistor R_G (usually large, $\approx$ M$\Omega$), so V_G=0 V (recall that due to the high input resistance we assume I_G=0). A current I_D will flow through R_D and R_S, so V_S will be positive. Thus V_GS is negative. Indeed, V_S = I_D R_S, and so

 

V_GS = V_G - V_S = -I_D R_S (120)

This equation as well as the square law

$$% latex2html id marker 927 I_{DS} = I_{DSS}(1- \frac{V_{GS}}{V_p} )^2 \eqno{(\ref{eq:jfet-id})}$$

(recall I_D=I_DS) must be satisfied, so that

$$I_{DS} = I_{DSS}(1 + \frac{I_{DS}R_S}{V_P})^2 .$$ (121)

This is a quadratic equation for I_DS. If I_D=I_DS and V_GS are determined, equation (120) is used to determine R_S.

The I_D-V_DS load line is given by

$$I_D = \frac{V_{DD} - V_{DS}}{R_D + R_S}$$ (122)

(check this!)

A slightly more complicated and useful bias network is the voltage divider bias   of Figure 133.

  

Figure 133: n-channel JFET voltage divider bias.

In this case, since I_G=0 the gate voltage is given by

$$V_G = V_{GG} = \frac{R_{G2}}{R_{G1} + R_{G2}} V_{DD}$$

and hence

 

V_GS = V_G - V_S = V_GG -I_D R_S . (123)

This equation as well as the square law (110) must be satisfied. The remaining calculations are similar to the self-bias case,

$$I_{DS} = I_{DSS}(1 - \frac{V_{GG}}{V_P} + \frac{I_{DS}R_S}{V_P})^2 .$$ (124)

In doing these calculations, one can solve the quadratic equation analytically, or use a graphical or computer method.

[ENGN2211 Home]