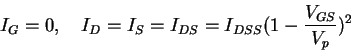[ENGN2211 Home]

Introductory FET Circuits

Consider again the circuit of Figure 123. We first do a DC analysis using the DC model of Section 9.3.1. You can either re-draw the circuit subsituting the model of Figure 127 for the transistor, or simply keep the same diagram and write explicitly the algebraic equations

$$I_G=0, \ \ \ I_D = I_S = I_{DS}= I_{DSS}(1- \frac{V_{GS}}{V_p} )^2$$ (115)

corresponding to the DC model.

Since I_G=0, the voltage drop across R_G is zero, and so V_G = V_GS=-V_GG; i.e. the gate-source voltage V_GS is determined directly as -V_GG due to the left voltage source. Now I_DSS and V_p are given parameters of the JFET, and so the drain current I_D can be determined from (115).

Next, KVL gives

V_DD = I_D R_D + V_DS

and therefore V_DS is given by

 

V_DS = V_DD - I_D R_D . (116)

This determines the operating or quiescent point Q.    

Graphically, we can plot the load line  

$$I_D = \frac{V_{DD} - V_{DS}}{R_D} .$$ (117)

on the I_D-V_DS characteristic, the intersection with the curve corresponding to the value of V_GS giving Q, see Figure 129.

  

Figure 129: JFET load line.

[ENGN2211 Home]