




[ENGN2211 Home]
Consider a signal f(t), a function of time t (e.g. a current
or voltage waveform), for positive times t.
The Laplace Transform of f(t) is a function F(s), where
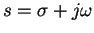 is a complex variable, defined by
is a complex variable, defined by
 = \int_{0^-}^\infty e^{-st} f(t) dt
\end{displaymath}](transimg22.gif) |
(19) |
We usually use capital letters to denote Laplace transforms.
The complex variable
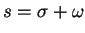 is called
complex frequency.
(Note that for AC steady state analysis, we use
is called
complex frequency.
(Note that for AC steady state analysis, we use 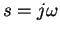 and don't use
and don't use 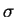 ;
see §4.1.)
;
see §4.1.)
In general there is a correspondance
and it is possible to find f(t) from F(s). These
are called Laplace Transform Pairs; an important example is
So if
F(s) = 2/(s+3), then
f(t)= 2e-3t for 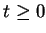 .
.
The Laplace transform is linear, which means that
So the Laplace transform of a superposition is the superposition of the
individual Laplace transforms.
We have seen that Ohm's Law for capacitors and inductors involves
derivatives. Let's see how derivatives transform:
 = s {\cal L}[f(t)](s) - f(0^-) .
\end{displaymath}](transimg30.gif) |
(20) |
The Laplace transform of a derivative is s times the Laplace transform
of the function plus the initial condition f(0-).
So if
f(t)= 2e-3t for 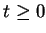 ,
then
,
then
=-6/(s+3)$](transimg31.gif) (check this both ways!).
(check this both ways!).
Electric circuits often have switches, and we can model switches
using a special function called the unit step function
u(t) defined by (see Figure 22)
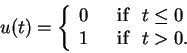 |
(21) |
Figure 22:
Unit step function.
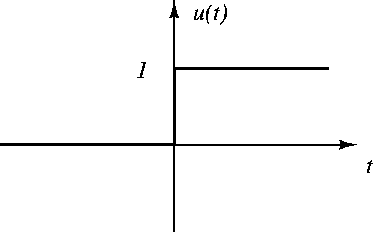 |
Exercise. Show that





[ENGN2211 Home]
ANU Engineering - ENGN2211
![]() is a complex variable, defined by
is a complex variable, defined by
![\begin{displaymath}\begin{array}{rl}
{\cal L}[af(t) + bg(t) ] & = a {\cal L}[ f(...
...[ g(t)]
\\ \\
{\rm or} & \\
& = a F(s) + b G(s) .
\end{array}\end{displaymath}](transimg29.gif)