[ENGN2211 Home]

Basic Definitions

  

Figure 39: Load absorbing power.

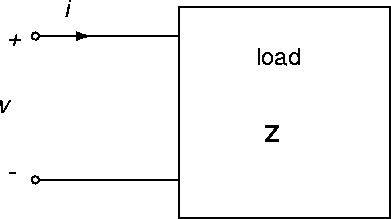Consider a load drawing a current i(t) with voltage v(t) across it, Figure 39. If v(t) and i(t) are periodic waveforms with period T, the instantaneous power   is

p(t) = v(t) i(t) .

It is also a periodic function.

The average power   is

$$P = \frac{1}{T} \int_0^T p(t) dt$$

(the average over one period).

If

$$v(t) = V_m \cos( \omega t + \phi_v), \ \ i(t) = I_m \cos( \omega t + \phi_i),$$

then $T=2\pi/\omega$ and

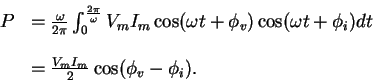$$\begin{array}{rl} P & = \frac{\omega}{2\pi} \int_0^{\frac{2\p... ...\ \\ & = \frac{V_mI_m}{2} \cos( \phi_v - \phi_i) . \end{array}$$ (49)

Real AC power is one half the product of the voltage and current magnitudes times the cosine of the angle between the voltage and current phasors.

If

$${\mathbf V} = V_m \angle \phi_v, \ \ {\mathbf I} = I_m \angle \phi_i ,$$

and

$$\theta = \phi_v - \phi_i ,$$

we can write

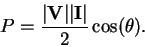$$P = \frac{ \vert {\mathbf V} \vert \vert {\mathbf I}\vert}{2} \cos(\theta) .$$ (50)

$\theta$ is called the power factor angle, and $\cos(\theta)$ is called the power factor.  

Note that P is the real power absorbed by the load.

The power P is a maximum when the power factor is 1, or $\theta =0$, i.e. the current and voltage are in phase.

[ENGN2211 Home]