Mathematica and Matlab Software for Computing Distance Distributions
During the course of my research, I have written a number of software libraries in collaboration with my students. One of them is now available publicly here and others will be made available in the future.
If you use the software in your research, please reference our relevant publication (see details below).
If you have any suggestions for improving the software, please email me and we can incorporate this in the software.
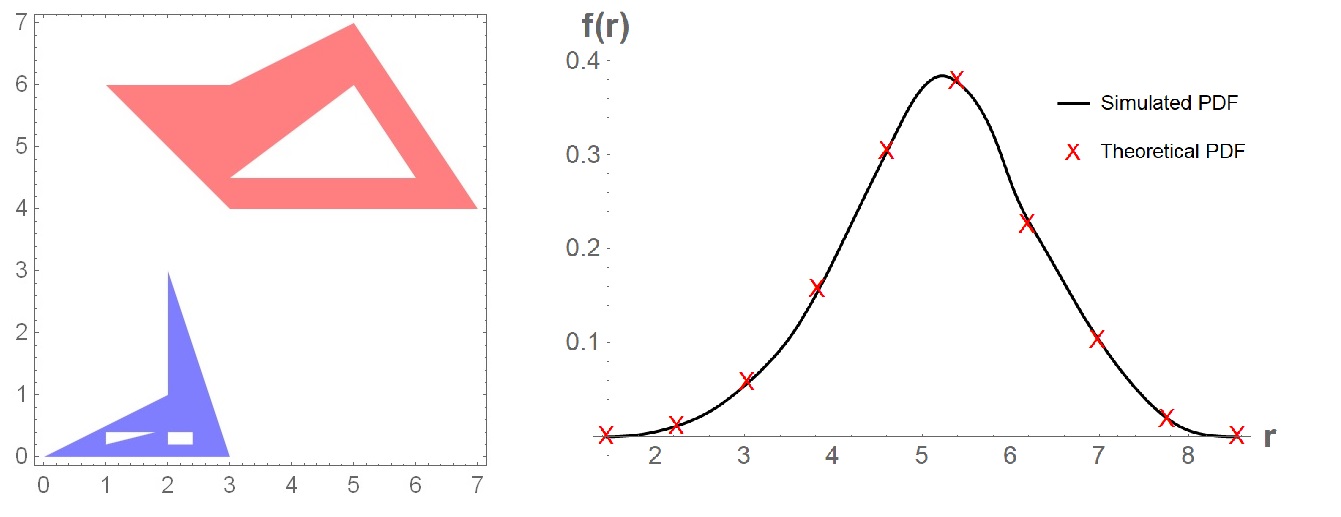
- Computing distance distributions between two random points, each uniformly randomly distributed in arbitrary (concave or convex) polygons with or without holes [Released: Jan. 2021]
- Mathematica Notebooks:
- Our paper is currently under review in Mathematical Methods in Applied Sciences journal (revised: 24 Jan. 2021)
- Screenshot:
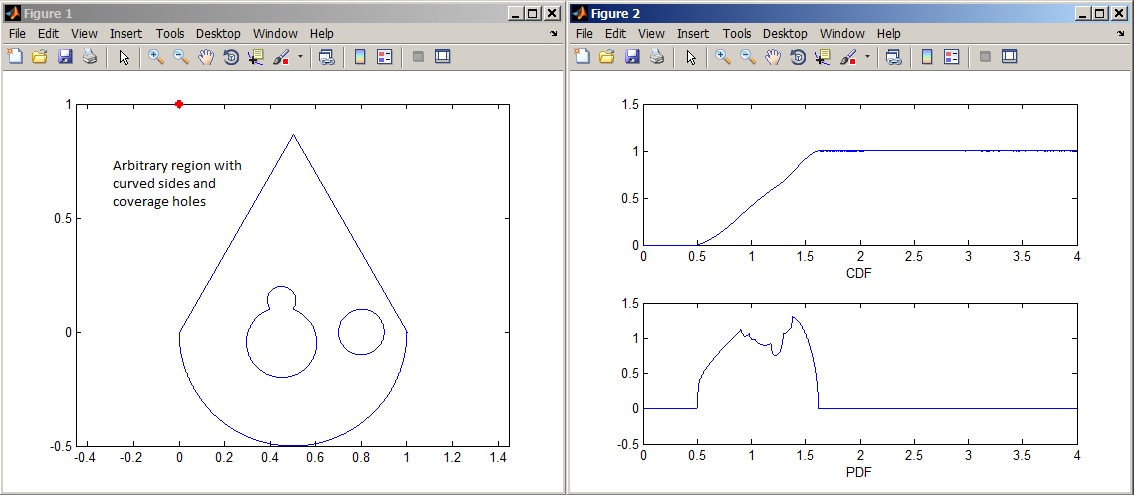
- Computing distance distributions in arbitrary (convex or concave) polygon regions with holes and arbitrary reference point [Released: coming soon!]
In K-tier heterogeneous networks, the coverage regions are modelled using a multiplicatively weighted Voronoi diagram. This software computes: (i) the exact closed-form probability density function and (ii) the exact closed-form cumulative density function of the distance between a randomly located node and any arbitrary reference point inside or outside an arbitrarily shaped multiplicatively weighted Voronoi cell.- Matlab code (zipped): Developed and tested [Nov. 2014].
- Mathematica code
- Our paper is still in draft form and I am hoping to write it up in the second half of this year.
- Screen shot:
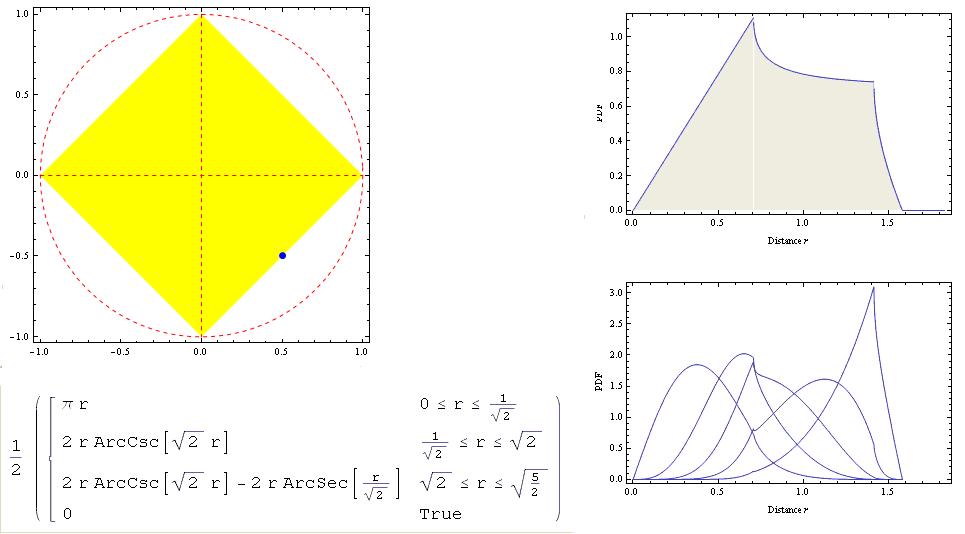
- Computing exact closed-form distance distributions in arbitrary (convex or concave) polygon regions without holes and arbitrary reference point [Released: June 2015]
This software computes: (i) the exact closed-form probability density function and (ii) the exact closed-form cumulative density function of the distance between a randomly located node and any arbitrary reference point inside or outside an arbitrary (concave or convex) polygon.- Mathematica Notebook
- Screen shot:
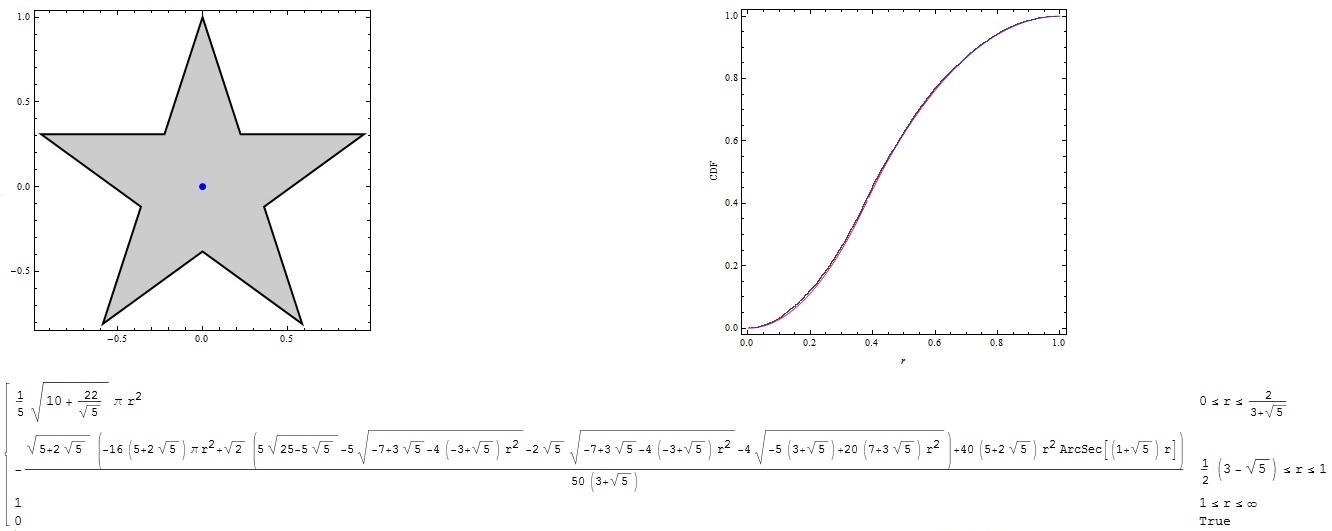
- Computing exact closed-form distance distributions in arbitrary convex polygon regions with interior reference point
This software computes: (i) the exact closed-form probability density function and (ii) the exact closed-form cumulative density function of the distance between a randomly located node and any arbitrary reference point inside an arbitrary L-sided convex polygon.- Our relevant IEEE TCOM paper (see Appendix A)
- Mathematica Notebook: This will no longer be posted. See our Mathematica Notebook, which can handle both concave and convex polygons.
- Computing exact closed-form distance distributions in regular polygon regions with interior reference point [Released: May 2013]
This software computes: (i) the exact closed-form probability density function and (ii) the exact closed-form cumulative density function of the distance between a randomly located node and any arbitrary reference point inside a regular L-sided polygon. These results can be used to obtain the closed-form probability density function of the Euclidean distance between any arbitrary reference point and its nth neighbor node when N nodes are uniformly and independently distributed (i.e. according to a uniform Binomial Point Process) inside a regular L-sided polygon. These distance distributions have many applications in wireless networks. This code is available in both Mathematica and Matlab.