 |
Here is the next state/output table for the up/down/stop counter example:
| Present state | next | state | output Y | |
| up | down | stop | ||
| s1 | s2 | s4 | s1 | odd |
| s2 | s3 | s1 | s2 | even |
| s3 | s4 | s2 | s3 | odd |
| s4 | s1 | s3 | s4 | even |
Compare this with the state diagram.
There are four states, so we need a minimum of two flip flops for the memory, which we label as AB. There are three input values, which we code using two bits SM, and two output values, coded with one bit labeled y.
Let's use the following binary coding:
| state | AB | input | SM | output | y |
| s1 | 00 | up | 00 | odd | 0 |
| s2 | 01 | down | 01 | even | 1 |
| s3 | 11 | stop | 1X | ||
| s4 | 10 |
With this coding, the next state/output table becomes:
| Present state | next | state | output | |
| up | down | stop | ||
| AB | S=0,M=0 | S=0,M=1 | S=1 | y |
| 00 | 01 | 10 | 00 | 0 |
| 01 | 11 | 00 | 01 | 1 |
| 11 | 10 | 01 | 11 | 0 |
| 10 | 00 | 11 | 10 | 1 |
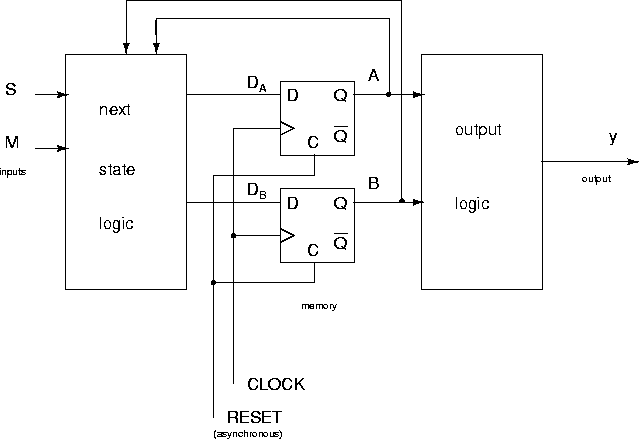
The general form of the circuit diagram for the state machine is shown in Figure 69. Here we have selected rising edge triggered D flip flops with asynchronous preclear as the memory elements.
The RESET signal is set up to force the state machine into a specified state, viz. s1=00.
Our job now is to work out the combinational logic required for the next state and output logic. To do this, we use k-maps, Figure 70.
We have used SM as entered variables. The k-map squares correspond to the four states (the k-maps are indexed by the state variables AB), and entries are obtained by a consideration of what the next state will be (from the next state table), and making use of the state transition table for the D flip flop.
The result is:
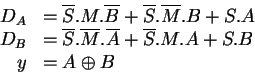
ANU Engineering - ENGN3213