[ENGN2211 Home]

Frequency Response

 

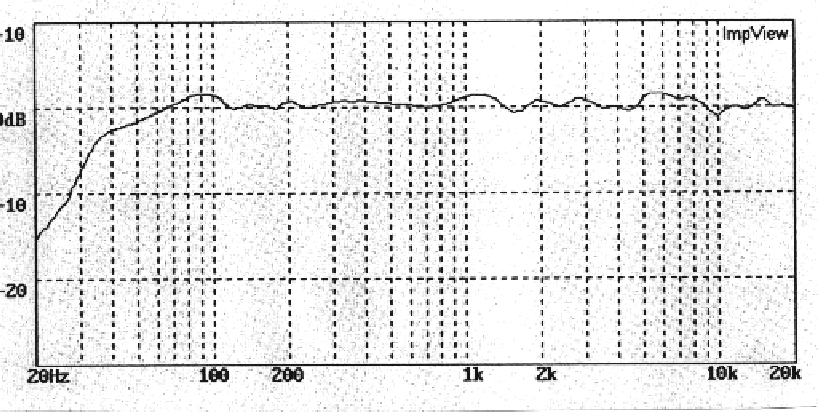
Frequency response is something that can be directly measured in the laboratory, with a sinusoidal source of variable frequency and an oscilloscope. The idea is to measure the magnitude and phase of the output relative to the input at a range of frequency values. If you have ever been shopping for a HiFi sound system, you may have seen frequency response diagrams in the promotional literature for speakers, amplifiers, etc, Figure 47.

  

Figure 47: HiFi speaker frequency response. (From Electronics Australia, Dec. 1998.)

The frequency response describes how a system responds to tones (pure sinusoids) at different frequencies.

Suppose that the input voltage is a complex sinusoid of frequency $\omega_{in}$:

$$v_{in}(t) = {\mathbf V}_{in} e^{j\omega_{in}t} \ {\rm V} ,$$

where V_in is a phasor. Then

$$V_{in}(s) = \frac{{\mathbf V}_{in} }{s-j\omega_{in}} ,$$

and so

$$V_{out}(s) = H(s) \frac{{\mathbf V}_{in} }{s-j\omega_{in}} .$$

After some calculations involving partial fractions, we find that (omitting transient terms)

$$V_{out}(s) = H(j\omega_{in}) \frac{{\mathbf V}_{in} }{s-j\omega_{in}} .$$ (59)

(Note the term $H(j\omega_{in})$.) Converting back into the time domain we get

$$v_{out}(t) = H(j\omega_{in}) {\mathbf V}_{in} e^{j\omega_{in}t} = H(j\omega_{in}) v_{in}(t) \ {\rm V}.$$ (60)

If we write $v_{out}(t) = {\mathbf V}_{out} e^{j\omega_{in}t}$, then in terms of phasors

$${\mathbf V}_{out} = H(j\omega_{in}) {\mathbf V}_{in} .$$ (61)

The output is the transfer function evaluated at $s=j\omega_{in}$ times the input.

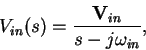
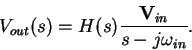
The function $H(j\omega)$ is called the frequency response function.   It is a function of frequency $\omega$ (rad/sec). We also write $H(j2\pi f)$ when we wish to use Hz.

[ENGN2211 Home]