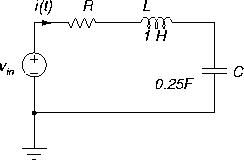[ENGN2211 Home]

RLC Dynamic Response

Load the series RLC circuit in PSPICE file rlc-trans.sch, Figure 24.

  

Figure 24: RLC transient.

Exercise:

1.

Simulate the circuit and obtain the transient response (current i(t)).

2.

Is the response underdamped, critically damped, or over damped?

3.

By trying various values of R, obtain all three types of responses: underdamped, critically damped, or over damped.

4.

In the underdamped case, determine the time constant $\tau$ and the frequency of oscillation $\omega = 2\pi f$ from your graph.

The current waveform is of the form

$$i(t) = Ae^{-t/\tau} \sin ( \omega t)$$

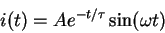
so you can find the values $\tau, \omega$ by measuring two data points for two successive peaks (where sine equals one), and doing some algebra:

Measure (i₁,t₁) and (i₂,t₂) at peaks (where $\sin (\omega t_1) = 1$, $\sin (\omega t_2) = 1$), form the ratio $i_1/i_2 = \exp(-(t_1-t_2)/\tau)$ and solve for $\tau$, and find $\omega$ using t₂-t₁=T, where T is the period.

Note that the peaks trace out an exponential envelope (like amplitude modulation).

5.

Compare with theory.

[ENGN2211 Home]