Quadratic program solver. More...

Inheritance diagram for drwnQPSolver:

Public Member Functions
	drwnQPSolver ()
	default constructor

	drwnQPSolver (const MatrixXd &P, const VectorXd &q, double r=0.0)
	construct an unconstrained QP

void	setObjective (const MatrixXd &P, const VectorXd &q, double r=0.0)
	set the objective function for the QP (dimensions must agree)

void	setEqConstraints (const MatrixXd &A, const VectorXd &b)
	set the linear equality constraints for the QP (dimensions must agree)

void	setIneqConstraints (const MatrixXd &G, const VectorXd &h)
	set the linear inequality constraints for the QP (dimensions must agree)

void	setBounds (const VectorXd &lb, const VectorXd &ub)
	set the upper and lower bounds for each variable, i.e., box constraints

void	clearEqConstraints ()
	clear the linear equality constraints

void	clearIneqConstraints ()
	clear the linear inequality constraints

void	clearBounds ()
	clear the upper and lower bounds on each variable

virtual void	initialize (const VectorXd &x)
	initialization (e.g., for warm-start methods)

virtual double	solve ()
	solve the QP and return the objective value

double	objective () const
	return the current value of the objective (this is the solution if the solve() function was previously executed and the problem has not changed)

double	objective (const VectorXd &x) const
	return the objective value for a given feasible point

VectorXd	solution () const
	return the current estimate of the solution

int	size () const
	return the number of dimensions of the state space

double	operator[] (unsigned i) const
	access the `i-th` dimension of the current solution

Static Public Attributes
static double	alpha = 0.3
	line search stopping criterion in (0, 1/2)

static double	beta = 0.5
	line search backtracking parameter in (0, 1)

Protected Member Functions
VectorXd	gradient () const

VectorXd	gradient (const VectorXd &x) const

bool	isFeasiblePoint (const VectorXd &x) const

double	solveOnlyBounds ()

double	solveSingleEquality ()

double	solveSimplex ()

double	solveNoBounds ()

double	solveGeneral ()

double	lineSearchNoBounds (const VectorXd &x, const VectorXd &dx, const VectorXd &nu, const VectorXd &dnu) const

double	lineSearchGeneral (const VectorXd &x, const VectorXd &dx, const VectorXd &nu, const VectorXd &dnu) const

void	solveKKTSystem (const MatrixXd &Hx, const MatrixXd &Hy, const MatrixXd &A, const VectorXd &c, const VectorXd &b, VectorXd &x, VectorXd &y) const

void	solveKKTSystem (const MatrixXd &Hx, const MatrixXd &A, const VectorXd &c, const VectorXd &b, VectorXd &x, VectorXd &y) const

Protected Attributes
MatrixXd	_mP
	positive definite quadratic term in the objective function

VectorXd	_q
	linear term in the objective function

double	_r
	constant term in the objective function

MatrixXd	_mA
	linear equality constraint matrix

VectorXd	_b
	linear equality constraint vector

MatrixXd	_mG
	linear inequality constraint matrix

MatrixXd	_h
	linear inequality constraint vector

VectorXd	_l
	variable lower bounds (box constraint)

VectorXd	_u
	variable upper bounds (box constraint)

VectorXd	_x
	current estimate of solution

Detailed Description

Quadratic program solver.

Solves (small scale) quadratic programs of the form:

$\begin{array}{ll} \textrm{minimize (over $x$)} & \frac{1}{2} x^T P x + q^T x + r \\ \textrm{subject to} & Ax = b \\ & Gx \leq h \\ & l \leq x \leq u \\ \end{array}$

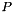where $P$ is positive semi-definite.

In the general case, the current implementation is based on the method of Hildreth and D'Esops:

C. Hildreth, A quadratic programming procedure, Naval Research Logistics Quarterly, 1957.
(see http://onlinelibrary.wiley.com/doi/10.1002/nav.3800040113/pdf)
D. A. D'Esopo, A convex programming procedure Naval Research Logistics Quarterly 6(1) 1959.

If no equality or general inequality constraints (not including bounds) are given, then the problem is solved in primal form. Otherwise, it is converted to the dual,

$\begin{array}{ll} \textrm{minimize (over $\lambda, \nu$)} & \frac{1}{2} (\lambda, \nu)^T \tilde{P} (\lambda, \nu) + \tilde{q}^T (\lambda, \nu) \\ \textrm{subject to} & \nu \geq 0 \\ \end{array}$

where

$\tilde{P} = \left[ \begin{array}{cccc} A P^{-1} A^T & A P^{-1} G^T & -A P^{-1} & A P^{-1} \\ G P^{-1} A^T & G P^{-1} G^T & -G P^{-1} & G P^{-1} \\ -P^{-1} A^T & -P^{-1} G^T & P^{-1} & -P^{-1} \\ P^{-1} A^T & P^{-1} G^T & -P^{-1} & P^{-1} \end{array} \right] \quad \textrm{and} \quad \tilde{q} = \left[ \begin{array}{c} b + A P^{-1} q \\ h + G P^{-1} q \\ -l - P^{-1} q \\ u + P^{-1} q \end{array} \right]$

The primal solution is retreived as 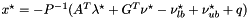$x^\star = -P^{-1}(A^T \lambda^\star + G^T \nu^\star - \nu_{lb}^\star + \nu_{ub}^\star + q)$ .

If no inequality constraints (including bounds) are given, then the code uses an infeasible-start newton method to satisfy the optimality conditions, i.e.,

$\begin{bmatrix} P & A^T \\ A & 0 \end{bmatrix} \begin{bmatrix} x \\ \nu \end{bmatrix} = \begin{bmatrix} -q \\ b \end{bmatrix}$

See:

S. Boyd and L. Vandenberghe, Convex Optimization, 2004.

Future versions may include specialized algorithms such as:

V. Franc and V. Hlavac. A Novel Algorithm for Learning Support Vector Machines with Structured Output Spaces, CTU-CMP-2006-04, May, 2006.
R. J. Vanderbei, LQOQ: An interior point code for quadratic programming, Technical Report SOR-94-15, Princeton University, 1998.

Warning: The QP solver is an experimental feature of the current version of Darwin.

Member Function Documentation

double drwnQPSolver::lineSearchGeneral	(	const VectorXd &	x,
		const VectorXd &	dx,
		const VectorXd &	nu,
		const VectorXd &	dnu
	)		const

protected

Todo:: implement

double drwnQPSolver::solveSimplex ( )

protected

Todo:: implement specialized simplex solver

The documentation for this class was generated from the following files:

drwnQPSolver.h
drwnQPSolver.cpp

Public Member Functions

Static Public Attributes

Protected Member Functions

Protected Attributes

Detailed Description

Member Function Documentation