[ENGN2211 Home]

Small Signal Amplifiers

 

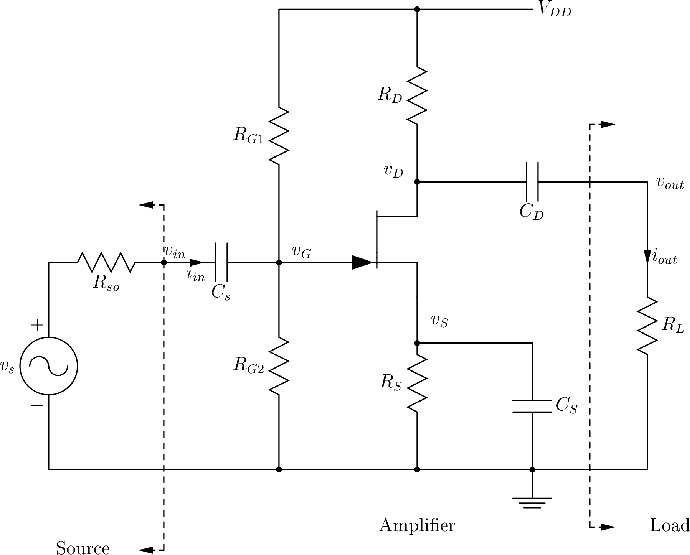
As an example of a FET amplifier, consider the JFET amplifier of Figure 136.

  

Figure 136: n-channel JFET small signal common source amplifier.

The JFET has parameters I_DSS=11 mA, V_p = -2 V. We will use the component values R_D = 1.2 k$\Omega$, R_S=680 $\Omega$, R_G1=5 M$\Omega$, R_G2=470 k$\Omega$, V_DD=30 V.

The voltage divider bias network gives

$$V_{GG} = \frac{470k}{470k + 5000k} 30 = 2.58 \ {\rm V}$$

and since I_G =0 we get V_G = 2.58 V. Now

V_S = I_D R_S

and so

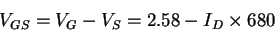$$V_{GS} = V_G - V_S = 2.58 - I_D \times 680$$ (128)

The square law (110) gives

$$I_D = 11\times 10^{-3}( 1- \frac{2.58 - I_D \times 680}{-2})^2$$

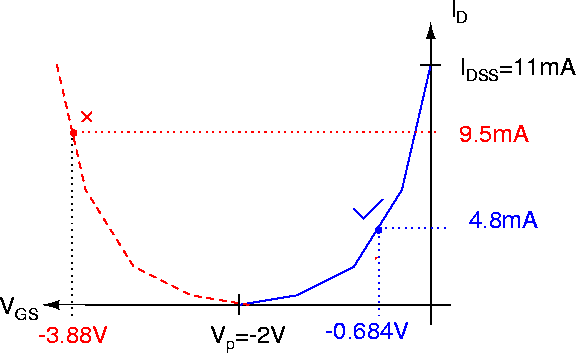
and solving this for I_D gives two solutions 4.8 and 9.5 mA. The smaller value is the correct one since the larger one is in a region where the quadratic formula is not a valid model. Why is this? Take a look at Figure 137 (the values of V_GS can be found using equation (128).

  

Figure 137: Square law and correct bias point determination.

Therefore

$$I_D = 4.8 \ {\rm mA}.$$

Next,

V_DD = I_D R_D + V_DS + I_D R_S

and so

$$V_{DS} = 30 - 4.8\times 10^{-3}(1200 + 680) = 20.98 \ V$$

This determines the DC operating point Q.

Now let's calculate the voltage gain

$$A = \frac{v_{out}}{v_{in}}$$

neglecting the influence of the source and load resistance.

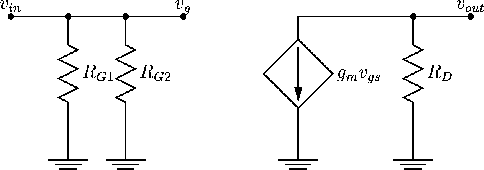
The source resistor R_S is short-circuited to AC signals by the bypass capacitor C_S, so the AC equivalent circuit is as in Figure 138.

  

Figure 138: AC equivalent circuit.

Now v_gs=v_in, and

v_out = - (g_m v_gs)R_D = - g_m R_D v_in .

Therefore

$$A = -g_m R_D = - (\frac{2 I_{DSS}}{\vert V_p \vert}(1-\frac{V_{GS}}{V_p})R_D)$$

and so A = -8.7.

It is straighforward to check that the input resistance   is given by

$$r_{in} = R_{G1} \parallel R_{G2} ,$$

and the output resistance is  

r_out = R_D .

Exercise. Find the gain from v_s to v_out including the effects of source and load resistances.

[ENGN2211 Home]