Excercise 2 - Social Network Anlaysis Questions
Note: Each of the following three questions is worth 1.0 mark. Answering any two of these three questions correctly will give you full mark on this part. The maximum mark you can get for this part is 2.0.
Question 3.1
Recall that the betweenness centrality of a node \(v\) is defined as: \[c_B(v)=\sum_{s,t \in V} \frac{\sigma(s,t|V)}{\sigma(s,t)} \] Now define the betweenness centrality of an edge \(e\) as \[c_B(e)=\sum_{s,t \in V} \frac{\sigma(s,t|e)}{\sigma(s,t)} \] here \(V\) is the set of nodes in an undirected graph, \(\sigma(s, t)\) is the number of shortest paths between node s and node t, \(\sigma(s, t|v)\) is the number of those paths passing through node v, and \(\sigma(s, t|e)\) is the number of those paths passing through edge e.
For an undirected network in the figure below.
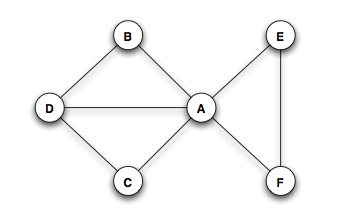
- Compute the (unnormalized) betweenness centrality for node A, B, and D.
- Which edge(s) has the highest and lowest betweenness centrality?
Question 3.2
An (undirected) tree is a connected, undirected network that has no cycles. Show that:
- A tree has at least two leaves, where leaves are nodes that have exactly one link.
- In a tree, there is a unique path between any two nodes.
Question 3.3
Recall from SMA lecture 1 that a shortest path between two nodes is a path of the minimum possible length. We say that a node X is pivotal for a pair of distinct nodes Y and Z if X lies on every shortest path between Y and Z (and X is not equal to either Y or Z).
- Give an example of a graph in which every node is pivotal for at least one pair of nodes. Explain your answer.
- Give an example of a graph having at least four nodes in which there is a single node X that is pivotal for every pair of nodes (not counting pairs that include X). Explain your answer.