next up previous contents index

[ENGN3213 Home]

Boolean Functions

NOT.  

\begin{displaymath}\overline{A} = \ {\rm NOT} \ A \end{displaymath}

So $\overline{A}$ is the complement of A, defined by the truth table  
A $\overline{A}$
0 1
1 0

A truth table defines the boolean function by specifying the boolean output value associated with each boolean input value.

The circuit symbol for the NOT function is the inverter, Figure 10.   The bubble denotes inversion (complement).


  
Figure 10: NOT gate.
\begin{figure} \begin{center} \epsfig{file=images/diglogimg1.eps}\end{center}\end{figure}

Interestingly, in Quantum Computing there is a $\sqrt{{\rm NOT}}$ gate, but that is another story.

OR.  

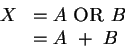
\begin{displaymath}\begin{array}{rl} X & = A \ \mbox{{\sc OR}} \ B \\ & = A \ + \ B \end{array}\end{displaymath}

Here + denotes OR, defined by:
A B X=A+B
0 0 0
0 1 1
1 0 1
1 1 1

OR is like two switches A, B is parallel; one or both open lets current flow. The circuit symbol is shown in Figure 11.


  
Figure 11: OR gate.
\begin{figure} \begin{center} \epsfig{file=images/diglogimg2.eps}\end{center}\end{figure}

AND.  

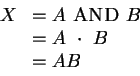
\begin{displaymath}\begin{array}{rl} X & = A \ \mbox{{\sc AND}} \ B \\ & = A \ \cdot \ B \\ & = AB \end{array}\end{displaymath}

Here $\cdot$ denotes AND, defined by:
A B $X=A\cdot B$
0 0 0
0 1 0
1 0 0
1 1 1

AND is like two switches A, B is series; both must be open for current to flow. The circuit symbol is shown in Figure 12.


  
Figure 12: AND gate.
\begin{figure} \begin{center} \epsfig{file=images/diglogimg3.eps}\end{center}\end{figure}

These three are the most basic logic functions, and define the Boolean algebra on the set ${\cal B}$.

Also important are the following functions.

NAND.  

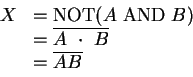
\begin{displaymath}\begin{array}{rl} X & = {\rm NOT} (A \ \mbox{{\rm AND}} \ B) \\ & = \overline{A \ \cdot \ B} \\ & = \overline{AB} \end{array}\end{displaymath}

NAND is defined by:
A B $X=\overline{AB}$
0 0 1
0 1 1
1 0 1
1 1 0

NAND is the complement of AND. The circuit symbol is shown in Figure 13. (We encountered the physical NAND gate in section 2.4.)


  
Figure 13: NAND gate.
\begin{figure} \begin{center} \epsfig{file=images/diglogimg4.eps}\end{center}\end{figure}

NOR.  

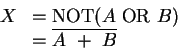
\begin{displaymath}\begin{array}{rl} X & = {\rm NOT} (A \ \mbox{{\rm OR}} \ B) \\ & = \overline{A \ + \ B} \\ \end{array}\end{displaymath}

NOR is defined by:
A B $X=\overline{A+B}$
0 0 1
0 1 0
1 0 0
1 1 0

NOR is the complement of OR. The circuit symbol is shown in Figure 14.


  
Figure 14: NOR gate.
\begin{figure} \begin{center} \epsfig{file=images/diglogimg5.eps}\end{center}\end{figure}

NAND and NOR are very important building blocks.

XOR.  

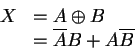
\begin{displaymath}\begin{array}{rl} X & = A \oplus B \\ & = \overline{A} B + A \overline{B} \end{array}\end{displaymath}

XOR is defined by:
A B $X=A \oplus B$
0 0 0
0 1 1
1 0 1
1 1 0

XOR is true if one and only one of A, B is true; hence the term exclusive OR.  . The circuit symbol is shown in Figure 15.


  
Figure 15: XOR gate.
\begin{figure} \begin{center} \epsfig{file=images/diglogimg6.eps}\end{center}\end{figure}

XOR is useful in

EQV.  

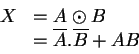
\begin{displaymath}\begin{array}{rl} X & = A \odot B \\ & = \overline{A} . \overline{B} + A B \end{array}\end{displaymath}

EQV is defined by:
A B $X=A \odot B$
0 0 1
0 1 0
1 0 0
1 1 1

EQV is true only if both A and B are the same, and so is the complement of XOR. It is called equivalence or exclusive NOR.   The circuit symbol is shown in Figure 16.


  
Figure 16: EQV gate.
\begin{figure} \begin{center} \epsfig{file=images/diglogimg7.eps}\end{center}\end{figure}

EQV is useful for detecting equality.

next up previous contents index

[ENGN3213 Home]

ANU Engineering - ENGN3213