[ENGN2211 Home]

Appendix: Complex Numbers

 

We write

$$j = \sqrt{-1} .$$

Of course, the basic principle is that

j² = -1 .

A general complex number has the form

z = x + j y ,

where

$$x = {\rm Re}(z)$$

is the real part of z, and

$$y = {\rm Im} (z)$$

is the imaginary part of z.

The complex number z can be plotted on the complex plane, with x as the x-axis (horizontal) coordinate, and y as the y-axis (vertical) coordinate.

We often use polar form,

$$z = \vert z \vert e^{j {\rm arg(z)}} = R e^{j\theta} = R \angle \theta$$

where

$$R= \vert z \vert = \sqrt{x^2 + y^2} ,$$

is the magnitude or modulus or length, and

$$\theta = arg(z) = \tan^{-1} (\frac{y}{x} )$$

is the argument or angle.

The conjugate 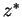$z^\ast$ of z=x+jy is defined by

$$z^\ast = x - j y .$$

Note that

$$z z^\ast = z^\ast z = \vert z \vert^2 .$$

Let

$$z_1 = x_1 +j y_1, \ \ z_2 = x_2 +j y_2 .$$

Addition/subtraction:

$$z_1 \pm z_2 = (x_1 \pm x_2) +j(y_1 \pm y_2) .$$

Multiplication:

z₁ z₂ = (x₁ x₂ - y₁ y₂) + j(x₁ y₂ + y₁ x₂)

or

$$z_1 z_2 = (R_1 R_2) \angle( \theta_1 + \theta_2 ) .$$

Division:

$$\frac{z_1}{z_2}= \frac{z_1 z_2^\ast}{\vert z_2 \vert^2} = (\frac{R_1}{R_2}) \angle( \theta_1 - \theta_2 ).$$

[ENGN2211 Home]