




[ENGN2211 Home]
You learned a bit about differential equations
in first year, and you will learn more in second
years maths. You will only need to solve some basic
differential equations in this course.
Here is a summary of some basics.
First Order Differential Equation:
Second Order Differential Equation:
General Solution:
x(t) = xh(t) + xp(t)
xh = complementary (homogeneous) solution,
i.e. the solution of the homogeneous equation (forcing term f=0):
xp= particular solution, the part that is determined by
the forcing term f.
Homogeneous Solution:
Trial solution
x(t) = Kest
Differentiate and plug into homogeneous equation gives
the characteristic equation
s2 + a1 s + a0 = 0
Two solutions
So homogeneous solution:
xh(t) = K1 es1 t + K2 es2 t
Re-write characteristic equation
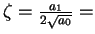 damping ratio
damping ratio
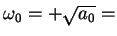 unforced natural frequency
unforced natural frequency
Write
Three cases:
- Overdamped
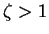 Two distinct real roots
Two distinct real roots
Homogeneous solution
- Critical damping
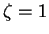 Two equal real roots
Two equal real roots
Homogeneous solution
- Underdamped
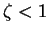 Two distinct complex roots
Two distinct complex roots
Homogeneous solution
Particular Solution: The trial form of the particular
solution xp(t) depends on
the forcing function f(t).
-
If f(t)=F a constant for all t, then try xp(t)=A another constant.
-
If
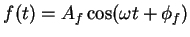 is sinusoidal, try
is sinusoidal, try
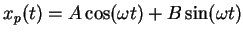 .
.
General Solution: the sum of the homogeneous and
the particular solutions
x(t) = xh(t) + xp(t) = K1 es1 t + K2 es2 t + xp(t)
Method of Solution:
To solve a linear differential equation with given
intital condition, the general method of solution
is:
- 1.
- Write down the characteristic equation and solve for the two
zeros s1 and s2.
- 2.
- Determine the form of the homogeneous solution
(Keat, Kteat,
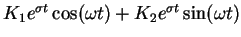 ,
etc) and write it down.
,
etc) and write it down.
- 3.
- Guess the form of the particular solution xp(t), based on the
form of f(t). Substitute xp(t) into the DE and find any
constants (A< B, etc) in your formula for xp(t).
- 4.
- Add the particular solution to the homogeneous
solution:
x(t)= xh(t) + xp(t)
and now use the initial conditions to determine the constants (K1,
K2, etc)
in the expression for the homogeneous xh(t). This can
only be done after any constants in the particular soilution
have been determined (in the previous step).
- 5.
- You now have the complete solution. As a check, plug it into the DE to
see if it is correct and also you can check the initial conditions.
- 6.
- Also, when solving circuit problems, is your solution consistent with
your intuition about how the waveform should look? Does your
solution agree with a spice or maple simulation?





[ENGN2211 Home]
ANU Engineering - ENGN2211
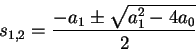
![]() damping ratio
damping ratio
![]() unforced natural frequency
unforced natural frequency