[ENGN2211 Home]

Active Filters

Filters constructed from resistors, capacitors and inductors are called passive,   since there are no active elements. Passive filters have the advantage of simplicity, but are incapable of amplification (gain is always less than one), and may require inductors which are relatively heavy and costly.

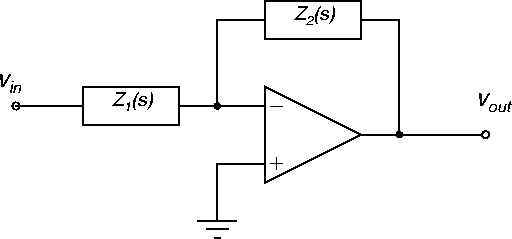
Active filters   contain an active element such as an operational amplifier, e.g. Figure 53. Active filter circuits can be used to implement a wide range of specs, do not need inductors, and can achieve gains greater than one.

  

Figure 53: Active filter based on inverting amplifier configuration.

The transfer function for the active filter of Figure 53 is

$$H(s) = - \frac{Z_2(s)}{Z_1(s)} ,$$ (65)

where Z₁(s) and Z₂(s) are s-domain impedances (check this). Filters are designed by choosing these impedances appropriately.

For a low pass filter, take Z₁(s) = R₁, $Z_2(s) = R_2 \parallel \frac{1}{sC_2}$.

For a high pass filter, take $Z_1(s) = R_1 + \frac{1}{sC_1}$, Z₂(s) = R₂.

Another active filter architecture is used in Hardware Lab 4.

[ENGN2211 Home]