Transmission line transformers are among the most amazing and exciting doodads in RF (for me anyway). They allow broadband functionality from low (kHz) to very high frequencies where some people think you would need active devices and lots of money. Transmission line transformers are usually wound on ferrites or powdered iron cores which are either toroidal or linear. Normally ferrites are the best choice for most broadband applications such as those for transmission line transformers.
I will not be labouring on about them in this course (for a good practical introduction see the book by Sevick. Here I will restrict myself to a short introduction to transformers, ferrites and three useful devices, all of which you have already met. These are the hybrid combiner (our voltage probe), the current transformer (the current probe) and the balun (available at Tandy's for adapting your 300 Ohm TV twin line to 75 Ohm coax).
The simple picture of a transformer is the following.
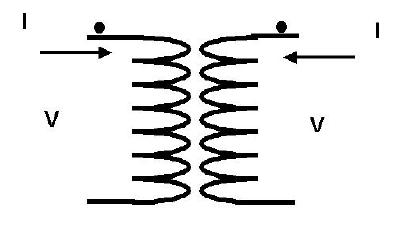
This is a 1:1 transformer (equal number of turns on the secondary and the primary). The dots indicate the sense of the windings. It is necessary at RF to wind the primary and secondary turns as a bifilar pair. This means that the wires are wound uniformly as would be the case of a transmission line. If the wires are touching, then the simplest choice is to twist them together before winding them on the transformer. Under these conditions the dots always appear at the same ends of the wires.
Transformers may be wound on both linear and toroidal ferrites. The latter are the choice for most applications due to their higher efficiency and better RFI performance; magnetic flux does not have to leak into the surroundings. The number of turns is simply determined by the range of frequencies over which the transformer is to operate. The low frequency performance is limited by how low an impedance the external circuit can tolerate. As we are about to see, the operation of a transmission line transformer in the simplest order requires that the reactance of the transformer using any winding must be much larger than the external circuit impedances.
The high frequency performance is most often limited by the operation of the wire pair as a transmission line and how the transmission line is used in the circuit. Clearly if the wires are wound together they make a pretty poor transmission line and parasitic L and C destroy the response at high frequency as it did in our first exercise on wires. The problem lies in irregularities in the line parameters which become more important at high frequencies. It is clear therefore that it would be best to make transmission line transformers using standard transmission lines, but this is not always practical.
Step one in the design is to calculate the impedance of a core at low frequency. To do so one may use the expression for a toroid of circumference l (or linear ferrite of length l), given by
L = m0mr N2 A/l
where m0 =4p x10-7W/m is the free-space permeabiliity and mr is the relative permeability. N is the number of turns and A is the (small) cross-sectional area of the toroid. To simplify calculations most manufacturers supply the value AL defined by L/N2.
In order to design a low power, broadband circuit with ferrites requires little more than knowledge of the AL value and the range of frequencies over which the ferrite can be used. Using the above L to obtain the low frequency impedance suffices because the impedance of the transformer increases with frequency and may even approach parallel resonance as we have seen and this is OK for transmission line transformers in that it has no adverse affect on performance. For high power applications or tuned applications where high Q is desired, care also has to be taken not to exceed the maximum flux density of the core and to take into account ohmic losses (such as bulk resistivity and hysteresis of the material).
Now usually powdered iron cores have lower losses and can withstand higher flux densities before core saturation and destruction than ferrites but this does not mean that they are the best choice for broadband RF applications at high power. The reasons are the following.
(a) The magnetic flux density problem leading to core saturation is something which is always worst at low frequency. This is because the voltage level on any winding port to ground is given by V ~ NwBA, where N is the number of turns, B is the flux density (Tesla), w is the (radian) frequency and and A the area of the core. As the highest flux density for a given power density therefore occurs at the low end of the frequency spectrum. Ferrites have higher relative permeability, mr , allowing smaller transformers to be wound at lower frequencies.
(b) Similarly, low bulk resistivity and hysteresis are not the only determining factors in core ohmic losses.
TRANSFORMER OPERATION
We now derive the simple formulae that determine the operation of the above 1:1 transformer.
Imagine that the above circuit is fed from a Thevenin source of voltage, v1, output impedance, Z1, and supplies a primary current, I1 to the transformer primary. This produces the secondary current I2 into the secondary from a load Z2. Notice that I am assuming that both currents flow into the dots on the transformers (a simple convention). The transformer can be described by its self reactance, X, and the mutual reactance, M. We also assume that the windings are such that these reactances are equal.
The primary and secondary equations are given by,
V1 - i1Z1 = jX(i1 + i2)
- i2Z2 = jX(i1 + i2)
We therefore obtain
V1 = i1Z1 - i2Z2
Now according to our design criterion at low frequencies, Z1,Z2 << X. Thus i1 + i2 = 0. We finally obtain
V1 = i1(Z1 +Z2)
This latter result is not of much use in its own right but helps us to uncover the main results: (1) Provided that for an n-filer 1:1 transformer, Z1,Z2,...,Zn << X, then SkIk = 0 where the Ik are the currents flowing into the "dots" i.e. are flowing in the same sense in the windings. There is a clear analogy of the 2-winding case with a transmission line for which we have been assuming that the current is equal and opposite in each line. (2) The voltages across all windings are equal because they are linked by the same magnetic flux.
The above analysis applies to a simple low frequency transformer. It could of course be extended by applying transmission line theory to the windings using the Telegraphist equations.