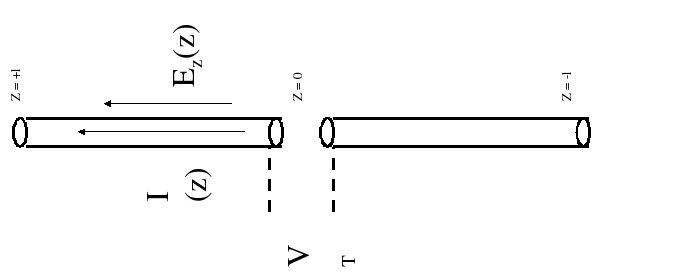
In the sections on impedance and networks we learned about two and four port devices. A single antenna is a two port device with a linear response to a voltage applied to it. A transmit and receive antenna pair is similarly a linear four port device. Thus, from the point of view of circuit analysis, we can expect to be able to treat antennas in exactly the same way as we do any other linear impedances or four port networks. For example, in order to model a circuit connect to an antenna, one can model the antenna by its Thevenin equivalent as follows,

where Z is the radiation impedance. What is the physical reason for this major simplification? It is of course very simple. All along you may have noticed that we have been disenfranchising circuit components of the status that they assumed at low frequencies. The first thing we did was to expose the parasitic components hiding inside resistors, capacitors and inductors. Then we introduced the concept of phase delay due to finite propagation speed. Here we idealised wires into transmission lines so that we could transport electromagnetic signals around circuits in a predictable way. Wires have now started to look rather complex. Antennas are the final step in this process of generalising wires. They are a simple extension of transmission lines and despite the fact that the laws that govern them are also applicable to transmisssion lines, we will see that they are much more general and powerful and are couched in situations which allow for the easy prediction of all the properties of antennas that we need. After all, antennas operate when exposed to external electromagnetic magnetic influences. Since electromagnetism is described by Maxwell's equations and these are themselves a linear set of equations, antennas can only exhibit a non-linear response if they themselves (or the external medium) contain non-linear materials. Since the latter is rarely the case, we can expect antennas to follow a simple linear circuit theory.
Antennas fall into two basic catagories: wire antennas and aperture antennas. Aperture antennas are antennas that behave more like optical lens and mirrors than wires. Since these are usually made of metal they are completely described by Ohm's law and hence are linear. The figures show the best known examples of wire and aperture antennas, namely the dipole/log-periodic wires of TV reception and a satellite dish aperture antenna.

 >
>
What antenna properties are we interested in? There are many properties that antennas have. In this short introduction we are going to cover the core properties that we need to completely describe a transmission-reception situation; i.e. the circuit analysis of antennas. Then we will look at radiation from antennas. Before discussing what properties we need to look at however, there are two surprising facts about antennas,
- All the basic universal properties that we need to describe antennas apply equally to wire and aperture antennas.
- The engineer does not have to know how to calculate the radiation pattern of an antenna in order to do point-to-point antenna transmission reception calculations in most cases. However radiation pattern calculation does provide a way of computing the impedance and gain of an antenna. And these are crucial parameters for circuit analysis involving antennas.
Note that there are many approaches to computing
the antenna radiation impedance. The most popular and widely used
methods are the Method of Moments (MoM) and the Frequency
Domain Time Domain (FDTD).
Antenna Properties
The properties of antennas that we will look at are,
- Antenna Radiation Impedance.
- Antenna Radiation Pattern.
- Antenna Gain.
- Friis Transmission.
- Antenna Aperture.
- Antenna Reciprocity.
In addition, antennas have the obvious property that they radiate electromagnetic waves. We will therefore have to look at how to compute the radiation of antennas.
Some Antenna ConceptsIn order to proceed and define these properties we first have to investigate the concept of an antenna. We have by now some understanding of the workings of transmission lines and the concepts of electromagnetic shielding. Taking these two together can help us to understand antennas.
Imagine that you take a twin wire transmission line as shown in the
following schematic. From a distance the closely spaced parallel lines
in the first figure look very close together. We do not expect this
system to radiate. We know however that there is a travelling wave
which propagates along this line at the speed of light with electric
fields as shown in red and currents flowing along the wire as shown in
green. Because the line is terminated in an open circuit, we know that
the voltage and current waves are reflected at the end and form
standing waves. We also know that the impedance is given by Z =
Zo/jtan(&beta l), where l is the length of the line. An
ideal line therefore has no resistance and therefore no losses.
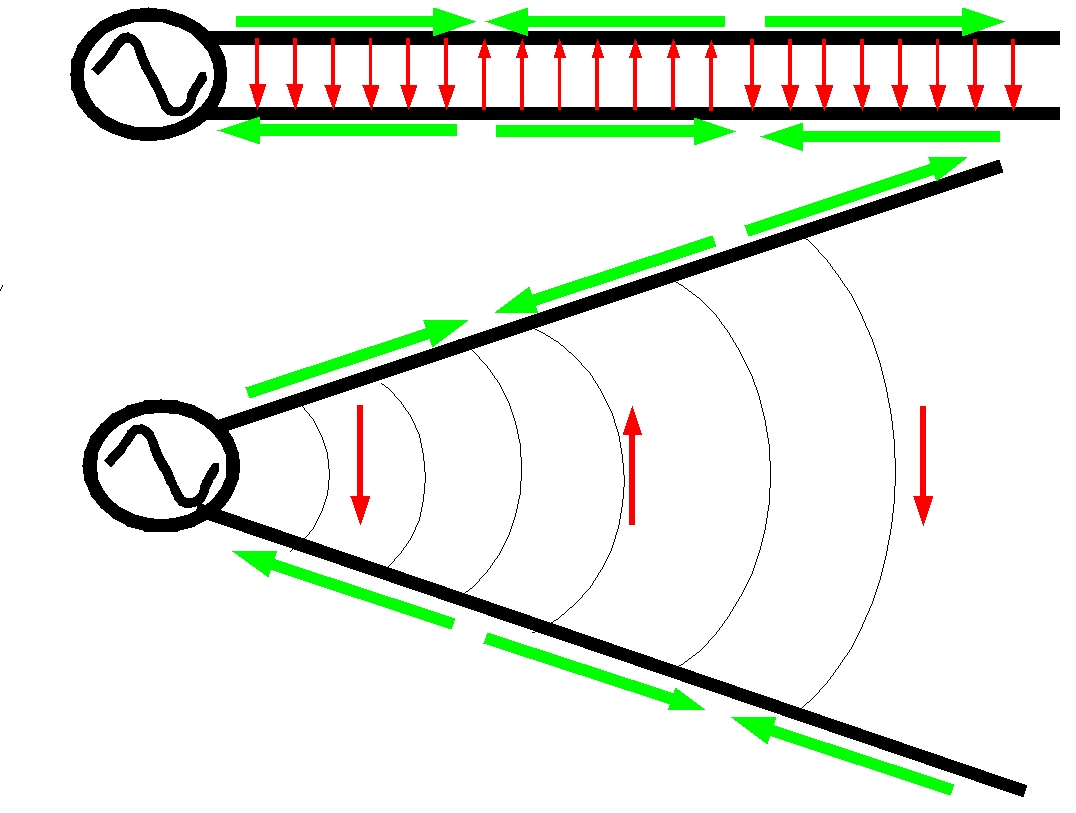
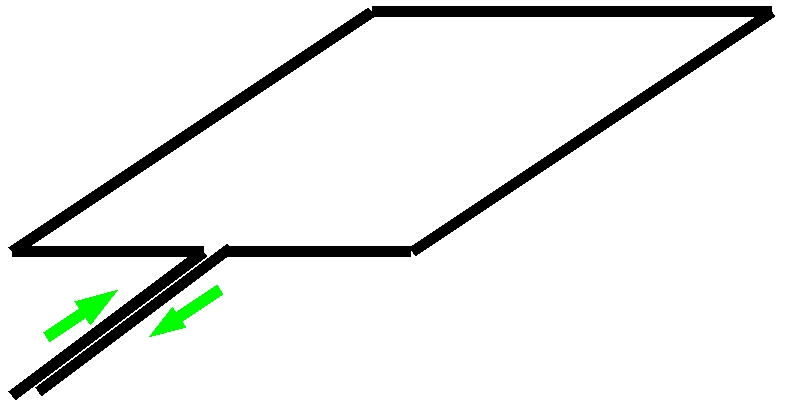
Now let's consider what happens if the line is opened up as shown in the second figure. Literally, the circuit is not altered, only that the two wire elements which form the line are now splayed. This is just how we make the most basic wire antenna, called a dipole by virtue of the fact that there are actually two elements due to the twin wires on the original transmission line. Notice that the new transmission line antenna has an opening angle. For a typical dipole we prise the elements completely apart so that the opening angle is 180o. An antenna with an opening angle less that 180o is in fact a viable directional antenna. Indeed a transmission line with a large separation between the parallel wires can radiate provided that the separation is not much smaller than a wavelength. Such an antenna is referred to as a travelling wave antenna.
There are a few things to notice about this new structure,
- The electric field lines are now arched rather than straight.They reach out into the space around the antenna. This effect is greatest when the opening angle is 180o as shown below for the case where there is less than a half a cycle along each wire.
- The currents still remain in the same relative direction and of the same order of magnitude. The current and voltage waves are still standing waves to a large degree. If the wires are filamentary and there is a single frequency exciting the antenna then the distribution of the current and voltage is still sinusoidal in shape. Note however that the currents do differ somewhat in amplitude from the transmission line because the impedance at the antenna terminals where the voltage sources connects to the wires differs in an important aspect from that of the transmission line.
- The antenna is now noticeable from a long distance away.
The most important thing to notice is that, by symmetry, the antenna is no longer a terminated line at all. Some of those E-field lines are going to be lost to the antenna because of the timelag effect in the oscillations. The easiest way to see this is to note that from a long distance, those antenna currents that used to be out of phase in the transmission line, have now been reversed. They are in phase and their distant E-fields now add.
These E-field lines now escape the system and lead to a loss in energy of the system. We say that the antenna radiates power in the form of electromagnetic waves. The following figure shows a dipole antenna. The direction of the current is shown in green. The electric field lines are marker in red. The plot to the right shows the current distribution along the antenna. Notice that the current drops to zero at the ends of the antenna as expected. Whether or not the current is a maximum at the source in the center of the antenna depends on the number of wavelengths along the antenna. The current is a maximum in the centre when the antenna is less than a half a wavelength long.
Not shown in the figure are the magnetic field lines. These are circles in the equatorial plane whose axis is along the antenna. As expected from simple magnetostatics, the magnetic field lines surround the current.
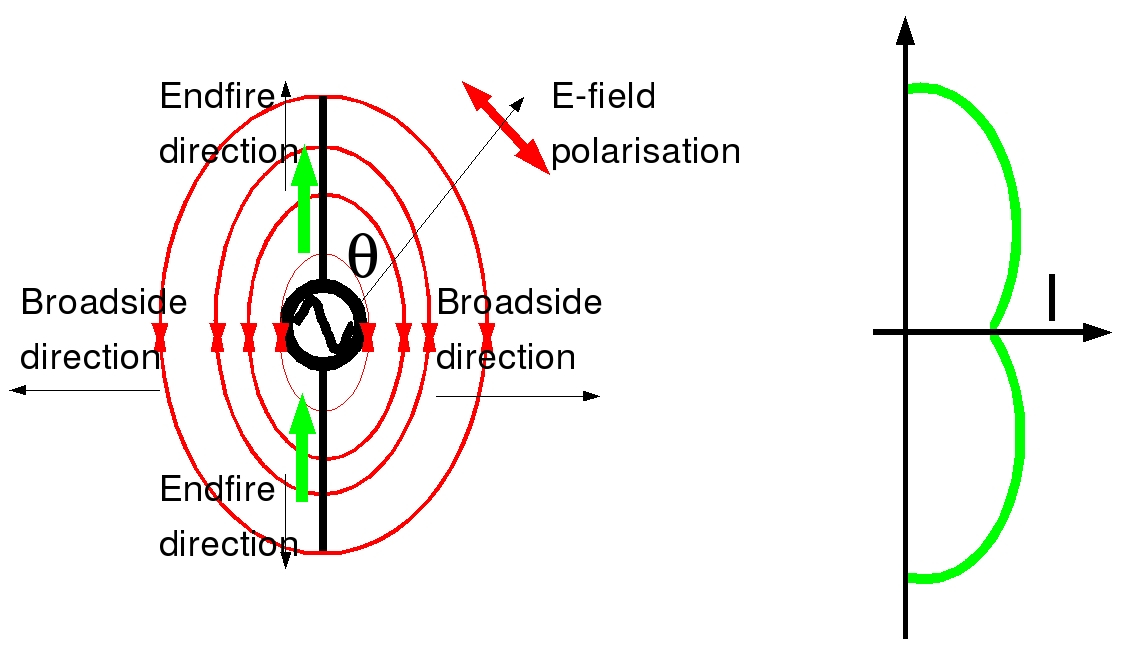
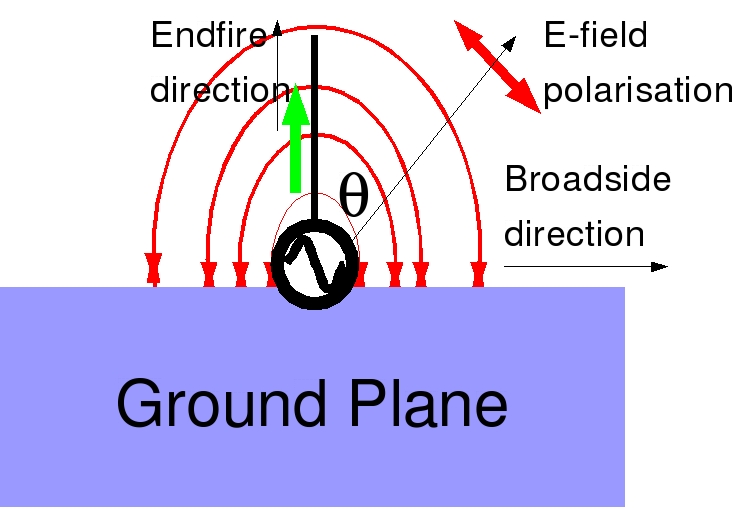
The same argument also implies that if power is lost then it must flow out in the general direction that is broadside to the antenna. There is no power flowing in the endfire direction. In fact the magnitude of the radiated field varies as sin(&theta), where &theta is the angle from the endfire direction to the point in field. Notice that it is the currents in the antenna that contribute to the radiation field and not the charge in the antenna. Although this is largely a mathematical point, the currents are the quantities that are seen from a distance. This is only the broadside direction which lies in the equatorial plane of the antenna. From the endfire direction (aimed along the wires), we see no oscillating current whatsoever. This may seem a bit strange given that the E-field in the case of the transmission line does in fact propagate along the wires.
The following figure shows the antenna radiation pattern of the dipole antenna. The green line represents the antenna at the center of the pattern. The radius vector from the center to the pattern at any given angle represents the amplitude of the electric field in that direction. The pattern can also represent the magnitude of the power flux density of the wave as well, but this is proportional to the square of the electric field. The figure on the right shows a schematic view of the magnetic field lines surrounding the antenna. The radiation pattern of the magnetic field is exactly the same as that of the electric field.
Finally there is one more qualitative conclusion. The direction in which the E-fields are aligned is always in the plane of the antenna currents and perpendicular to the radius vector of the point in the field. We say that the E-field has linear polarisation.
The above conclusions are true for any wire antenna. If, like the TV antenna, there are many such elements, then the above conclusions hold true individually for any wire element forming the antenna.
Antenna Impedance and Radiation PatternAll antennas have impedance. When a voltage is applied to the terminals of an antenna, there is a current which flows in response. Despite this obvious statement, there are some tricky issues.
The first is to define what we mean by the antenna terminals.
Dipole antennas . The dipole is the basic wire antenna. It consists of two straight wire sections mounted in a line and fed at the centre as shown above. The wires can be made of copper or aluminium for lightness. As a result, the ohmic resistance of these metals can never be a significant fraction of the resistive part of the radiation impedance or the antenna will be lossy. Dipoles are the building blocks of all wire antennas. The one discussed above is terminated in an open circuit at each end. This is not necessary and dipoles that are closed (both ends connected to each other) are referred to as magnetic diples as shown below. The open circuit variety shown above is referred to as an electric dipole.
The terminals of the various dipole types are clear from the above discussion. Things to note are that they are symmetric. This means that they are push-pull: they have to be driven with voltages that are 180o out of phase. This is just the same as in the case of the transmission line. Unfortunately this implies that some sort of transformer such as a balun will be needed if the transmission line feeding the antenna is not already symmetric. Secondly of course, stray inductance matters and so you should be careful about what part of the connector is in the antenna and what is part of the feeder.
No antenna discussion would be complete without the most useful form of dipole antenna. Let us consider what happens if the top half of the dipole antenna is retained but the bottom half is replaced by a direct connection to a ground plane as shown in the following figure. As shown in the figure at the right we now have a particularly convenient connector arrangement. The centre conductor of the source is connected to the element but the ground return connects to the ground plane. An implementation of this is shown in the third figure where a coaxial cable is connected to a ground bulkhead and an N-type connector onto which the antenna can be screwed. To see actual implementations of this have a look at the POLARELEC aerials in the comms lab. These aerials shown in the figure below screw into a magnetic base so that a much larger magnetic metal surface like the chassis of a car can be used as the ground plane. Obviously the conductivity of ground and the continuity of the connection to ground are crucial. Such single ended dipoles are referred to as monopoles and these are very popular because they are only half the size of a dipole and do not need a balun.
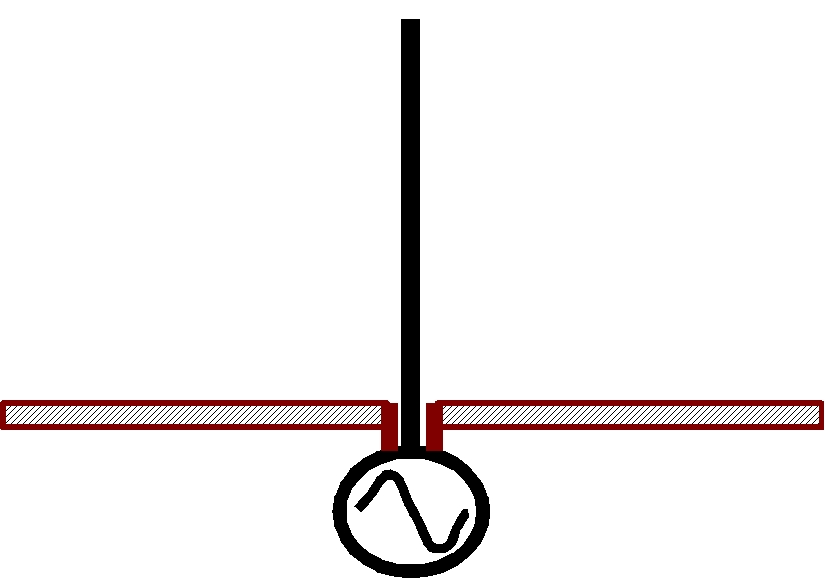
How do they work? Assuming that we understand how the dipole works then it is quite easy to explain monopoles. The earth plane acts as a mirror in effect. The lower element now appears as an image of the upper element. This means that the currents in the earth plane look like a monopole buried in the earth plane. Thus as far as an observer in the space above the earth plane is concerned, The antenna still looks like a dipole.
The following figure shows a monopole mounting fixture. The cable from the exciter is coaxial and its outer conductor terminates on earth. The center contact connects to the monopole element directly. Any series inductance with the element can be tuned out by shortening the monopole slightly to make it just capacitive enough to cancel the series inductance. The monpole acts like an extension of the centre conductor of the antenna. This is strange because the coaxial cable feeding the monopole itself has an equal and opposite current flowing on the inside of the outer conductor up to the point where it connects to the monopole element. So the question is what becomes of this current at the antenna-cable interface?. Obviously this current supplies the image currents referred to above. In order for this to occur successfully there must be enough earth to support the current. How much earth is enough and what happens if we dont have it? The second question is easier to answer. In the absence of earth one can expect that the return current from the inside of the outer conductor returns on the outside of the outer conductor and therefore heads back to the exciter. This situation is usually undersirable because, even though the antenna still radiates, its radiation impedance now includes an extra term due to the standing point impedance of this current to ground (whereever that may be!). In this situation, neither the radiation impedance nor the antenna pattern are predictable. It should be pointed out that when a high level current feeding an antenna at high power follows the coax feeder back to the exciter in this fashion, it also presents a radiation burn hasard to the equipment operator.
How much earth is enough? The ground plane into
which the coax bulkhead connects

Now we continue our discussion of antenna impedance. The resistive part of the antenna impedance is due to radiation. Electromagnetic waves launched by an antenna carry energy away from the antenna in just the same way that current flowing into a resistor carries power into the resistor from the power supply source. There is no formal difference between the physical process in the case of the resistor and the case of an antenna. Within the resistor the power is dissipated as heat. The antenna on the otherhand scatters the energy as electromagnetic radiation. Antennas look like resistors (though reactive ones) to the exciter. The electromagnetic waves launched by the antenna propagate away from the antenna at the speed of light carrying the energy with them.
In the limit where the antenna element is short in comparison to a wavelength, the electric field launched by a dipole is given by, Ep = 60jkexp(jkr)sin(Theta)/r, where k = 2 pi f/c, Theta is the angle between the endfire direction or the dipole axis and r is the radius to the point in the field from the centre of the antenna.
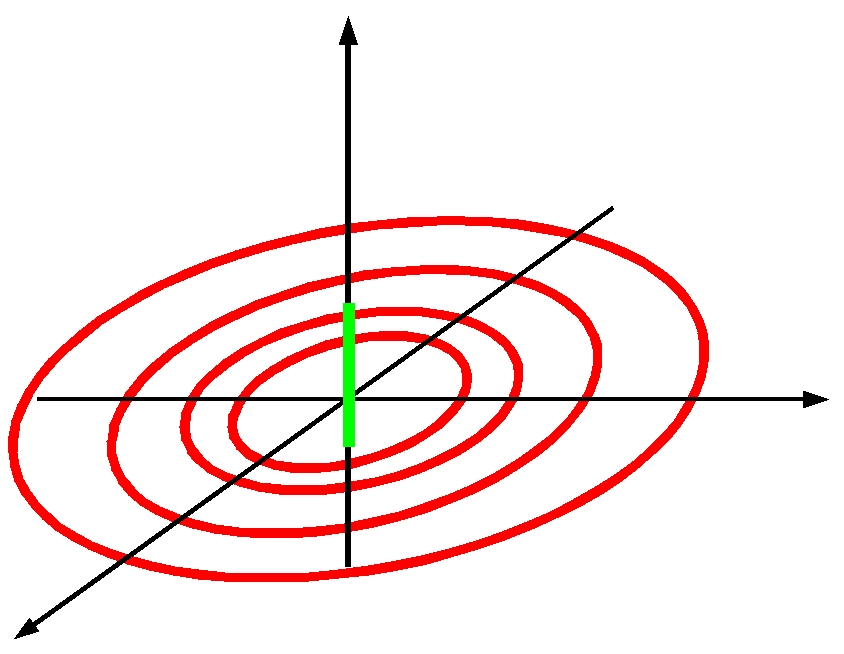
The waves propagate away on spherical wavefronts of constant phase as shown in the following figure. The dipole (monopole) is located at the origin and is oriented along the y axis (vertical). The animated contours are the electric field lines due to the dipole. Near the dipole, the field lines are essentially those of a static dipole leaving a positive charge and ending up at a negative charge. However, at a distance of the order of half wavelength or greater, the field lines are completely detached from the dipole. This detachment characterises radiation fields which propagate freely (without being attached to charges) in free space. The phase fronts shown in the figure advance at the speed c.
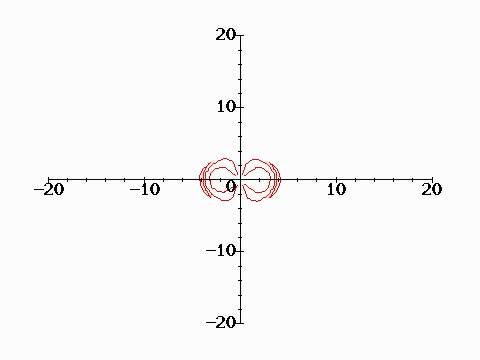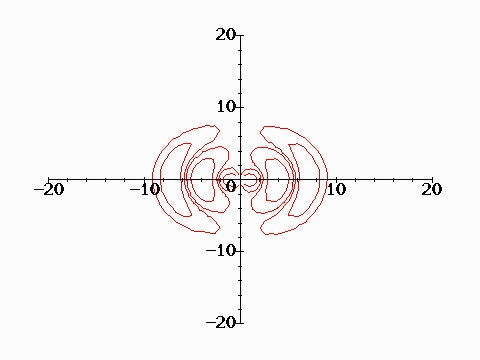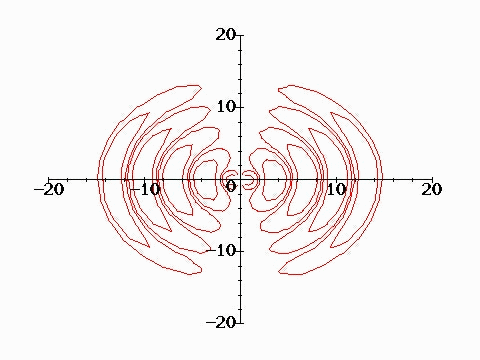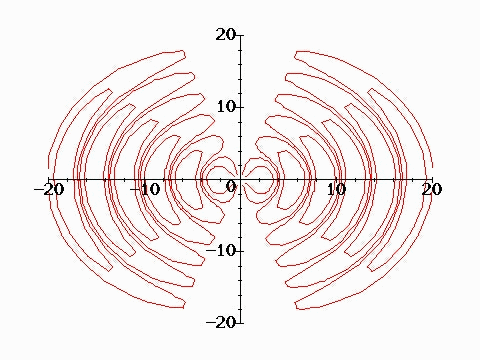
The radiation pattern is the angular pattern of radiation of these wavefronts. There are a number of waves of specifying the radiation power. Three are common.
- A plot of Ep versus angle from the endfire direction.
- A plot of power flux versus angle from the endfire direction.
- A plot of power flux in dBi versus angle from the endfire direction.
In the first, the electric field component perpendicular to the direction of propagation and in the plane of the dipole is what is referred to. At large enough distances from the antenna this is the only component of the E field left. In the second the power flux also known as the Poynting flux is plotted. The Poynting flux is given by P = Ep2/(2muOc) where muO is the permeability of free space.
The third uses the dBi which is the decibel ratio of the power flux in the field to that of a theoretical isoptropic radiator with the same power at the exciter. An isotropic radiator is one which radiates equally in all directions. The radiated power at any point a distance r from an isotropic radiator is given by S = Po/(4 pi r2). Note that the isotropic radiator is a hypothetical but useful abstraction as we are about to see.
The dBi pattern peaks at 2.14 dB for a dipole (monopole). The maximum value of pattern amplitude in dBi must be subtracted from the legally allowed Equivalent Isotropic Radiated Power for the frequency of operation in order to determine the maximum RF power of the exciter. The EIRP is a power that is chosen to represent the maximum permissible power flux of an antenna. The EIRP limits the maximum power flux of an antenna to that radiated by an isotropic radiator. For example if 30 dBm is the EIRP for the 27 MHz ISM band, then the maximum exciter power for a monopole is 30 - 2.14 = 27.86 dBm.
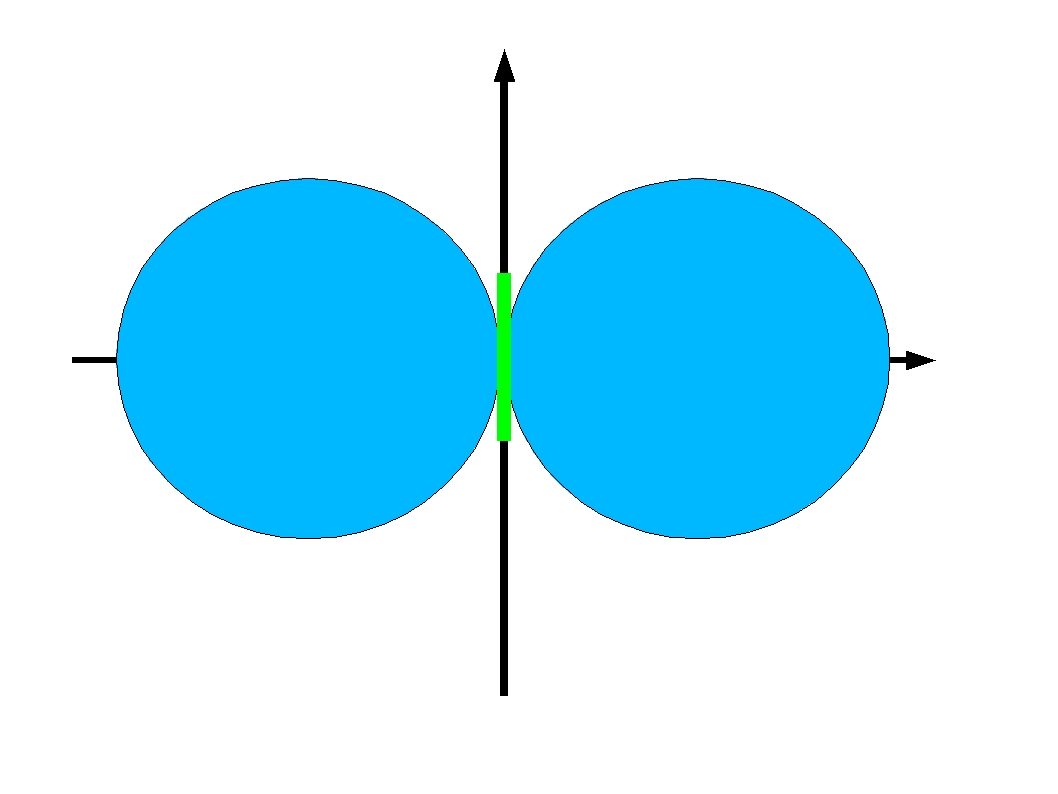
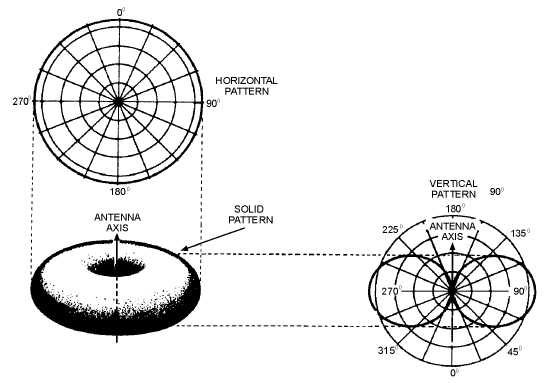
The following pattern summarises the pattern of the dipole. As you can see it depends on the plane it which it is observed. In the plane of the element, the pattern has the form in the above animation. However in the equatorial plane the pattern is uniform. In three dimensions the pattern overall looks like a donut.
Before leaving this section I present a MATLAB GUI that will allow you to compute the antenna impedance and radiation pattern of a monopole. The program is called zgui.m and can be downloaded from here. It is pretty easy to use and I am also pretty sure that it works. Be sure to read the README file which explains all about it. One interesting thing about this program is that it allows you to compute the radiation impedance and pattern for either metal or plasma patterns.
As explained in the README file zgui calculates the current profile along the antenna and hence radiation impedance from the Hallen Equation (see the book on antennas by J.D. Kraus) which is an integral equation evaluate along a dipole as shown in the figure. The real part of the impedance is confirmed by an independent calculation of the radiation resistance by an integration of the Poynting flux. A screen shot of zgui is shown in the following figure. To use it just click on either metal or plasma in the listbox at the top right.
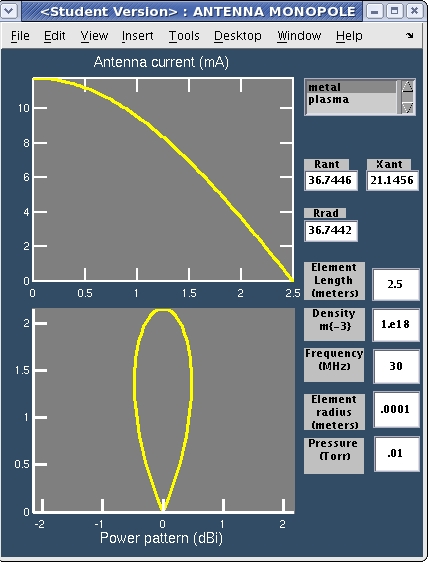
GUI front end to zgui which can be downloaded here.
By running zgui you can check that at quarter wave resonance the monopole has a resistance of 36 Ohms which is exactly half of the 72 Ohms of a quarter wave dipole. Moreover the radiation pattern of the dipole and the monopole are the same. The latter is not true however if the monopole has an inadequate earth.
Antenna GainNow we are ready to define antenna gain. Despite the fact that antennas are passive circuit elements, the still have gain. The antenna gain is the ratio of the maximum power flux of an antenna's radiation pattern to that of the isotropic radiator. In fact it is just the antenna's maximum dBi value: G = max(dBi).
Friis or Line-Of-Sight Transmission and Antenna Effective Aperture.The definition of antenna gain leads to an incredibly useful formula for the maximum power flux or Poynting flux radiated by an antenna: that is, the maximum power per unit area over all directions. Given the antenna gain we may say that the maximum power flux radiated by an antenna is given by combining the definition of gain with the power of an isotropic radiator to obtain Smax = GPo/(4 pi r2) where r is the radius in the field at which the power flux is desired, Smax is the power flux in Watts per meter squared and Po is power at the antenna terminals due to the exciter in Watts.
Note that by virtue of its simplistic nature this formula can only strictly apply in a Line-Of-Sight or LOS environment. It cannot be used under most circumstances indoors unless the transmit and receive antennas are much closer to each other than the nearest wall. It works very well however for describing satellite to earth communications and is widely used in so called link budget calculations.
So far I might have given the impression that all one can do is compute the fields radiated by antennas. In fact calculating the power received is just as easy and leads to a very surprising result. Consider an antenna immersed in a radiation field. As in the case of Friis transmssion let us assume that the receiving antenna has been oriented to receive maximum power. Obviously the antenna sees a power flux density and we call it S. The notion of antenna aperture is that the receiving antenna has a certain capture area Ae. The amount of power captured by the antenna is then given by Pr = S Ae.
But does the antenna really capture all of this power? In a sense the answer is YES. It really is this simple. However in addition to the fact that the antenna has to be correctly oriented, there are two subtleties. First the receiver that is intended to receive the power must be matched to the radiation impedance of the antenna i.e. it must have an input impedance that is the complex conjugate of the antenna radiation impedance. This is an obvious requirement. The second is Thevenin. Have a look at the Thevenin equivalent circuit at the top of this page. Clearly the output impedance (radiation impedance) of the antenna must share the power with a matched receiver. We therefore expect that the receiver can at most receive a half of the captured power. What happens to the other half?
How do we calculate Ae? Believe it or not for any antenna the antenna aperture Ae is given by Ae = G Lambda2/(4 pi). This amazing formula which I prove below says that the aperture is dependent only on the gain of the antenna (since wavelength is a property of the electromagnetic wave and not the antenna). Note at least that it is consistent with the antenna being oriented for maximum reception in as much as the antenna is also oriented for maximum transmission i.e. gain.
This simple formula is true for all antennas. It is easy to provide a heuristic proof for dish antennas such as those used for satellite reception. Consider a dish of area A and diameter d. Intuitively we expect that the effective aperture is the same as the geometrical aperture: A = Ae = pi d2/4. The gain of such a dish is given by the formula for the Rayleigh diffraction limit which says that the angular beamwidth of radiation emitted by a dish is given by Dtheta = 4 Lambda /(pi d) where d is ths dish diameter. The gain can be written as G = 16/Dtheta2 (i.e. the ratio of 4 pi solid angle to the area of a cap subtended by a full angle Dtheta). Elimination of Dtheta leads to G = (pi d /Lambda)2 and A = pi d2/4 = G Lambda2 / (4pi). In the next section we see why this simple formula applies to any antenna.
Now that we have covered LOS transmission and the effective aperture we are in a position to provide a formula to predict the complete coupling between a transmitting and receiving antenna. In order to do so we have to assume that the transmitting antenna is oriented so that its maximum power flux is radiated toward the receiving antenna and the receiving antenna is oriented to pick up the maximum signal from the transmitter. The LOS formula says that S = GTPo/(4 pi r2) where GT is the gain of the transmitting antenna, Po is the power of the exciter and r is the distance between the transmitter and receiver. The power captured by a suitably oriented receiver is Pr = AeS. Combining these we obtain, Pr = GT Ae Po/(4 pi r2).
Substituting for Ae = GRLambda2/(4 pi), we obtain PR = GTGR Po (Lambda/ (4 pi r))2. This is the Friis trasnmission formula. Note that it can written as a loss in dB, Ploss = 10log10(PR/Po) = 20log10(Lambda/ (4 pi r)). This is the most important formula for calculating link budgets. The Friis transmission formula constitutes the formal definition of free space path loss. Needless to say it only works for LOS links. Any other type of link will need a much more complex analysis involving diffraction effects. When the channel is not known a statistical calculation is required.
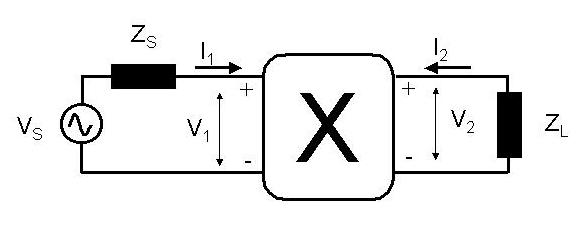
Antenna Reciprocity.The final topic on antennas is perhaps not a very surprising one: reciprocity. Reciprocity can already be anticipated on the basis of the symmetry of four port passive networks. Consider the definition of the y-parameters,
I1 = yiV1 + yrV2
I2 = yfV1 + yoV2
If we place a short across the second port so that V2 = 0 then the current that flows in the second port in response to a signal V1 applied at the first port is I2 = yfV1. Vice versa if we place a short across the first port so that V1 = 0 then the current in the first port that flows in response to a signal V2 applied at the second port is I1 = yrV2. You may have noticed in your work that provided we deal with passive networks (for example filters) the y-parameter yf = yr. This simple fact embodies the reciprocity theorem.
Notice that this equality between yr and yf does not apply to transistors. Nor does it apply in the presence of any kind of similar anisotropy in the system. In the case of transistors, the anisotropy arises from the difference in the forward and reverse transfer gains of the transistor: in other words normal transistor action. Other examples include magnetised ferrites and plasmas which are anisotropic media. Wave propagation in these media does not in general obey reciprocity.
One way of stating the reciprocity theorem is as follows. If we have two antennas, one at each end of a link, and we apply a voltage directly to the terminals of one and short the terminals of the other then the ratio of the exciting voltage in the transmitting antenna to the current across the terminals in the receiving antenna remains the same when the roles of the antennas are interchanged.
More generally it can be stated that if one antenna is excited with a Thevenin source of open circuit voltage VT and an output impedance ZT and the other antenna is terminated in ZT producing a current IR, then the ratio VT/IR remains the same when the Thevenin source and terminating impedance ZT are interchanged. This can be readilyproven from the above equations for the y-parameters with the assumption yf = yr.
The reciprocity theorem leads to an important result concerning the antenna effective aperture. Suppose that we consider a transmission experiment between an arbitrary antenna and a dish. In line with the above statement of the reciprocity theorem, let the antenna be excited by a Norton current source (ZT = infinity) of current IN and leave the antenna terminals open circuit. This corresponds to the Thevenin statement of the reciprocity theorem except that the impedance is infinite. If the real part of the impedance is Rant then the power radiated by the antenna is Pant= IN2Rant/2. The power intercepted by the dish is, PR_dish = GantAe_dishPant/(4 pi r2). The effective aperture of the dish, Ae_dish = Gdish Lambda2/(4 pi), so that PR_dish = Gant GdishLambda2Pant/(4 pi r)2. = Gant GdishLambda2IN2Rant/2/(4 pi r)2.
Since the dish must be left open circuit we need to compute the open circuit voltage of the dish due to this intercepted power. Using the reciprocity theorem, we know that the ratio of the current in the transmitter to this open circuit voltage must remain constant. If the dish impedance is matched to its load then Zload*=Zdish.In this case, the total series resistance is 2Rdish so that VOC_dish = 2sqrt(PR_dishRdish) and hence PR_dish = VOC_dish2/4/Rdish.
Now take the Norton current source to the dish. The power radiated by the dish is Pdish= IN2Rdish/2. The power intercepted by the antenna is PR_ant = GdishAe_antPdish/(4 pi r2) = GdishAe_antIN2Rdish/2/(4 pi r2).
Similarly the power intercepted by the antenna can be expressed in terms of the open circuit voltage developed as follows PR_ant = VOC_ant2/4/Rant.
The reciprocity theorem states that IN/VOC_ant = IN/VOC_dish or VOC_dish = VOC_rant and hence that PR_antRant = PR_dishRdish.
Thus the reciprocity theorem leads to the following equality: Gant GdishLambda2IN2/2/(4 pi r)2 = GdishAe_antIN2/2/(4 pi r2) which simplifies to Ae_ant= GantLambda2/(4 pi).
We conclude that the formula for the effective aperture: Ae_ant= GantLambda2/(4 pi) applies to ANY antenna. It is interesting to note that the somewhat long winded proof provided here seems superfluous given that the relation is self evident due to lack of details in the formula specific to any particular antenna.