

Next: Generating The Images
Up: Translating SAT Instances to
Previous: Translating SAT Instances to
There are a number of relationships in a SAT instance that could be represented by a
graph, and variations on these are also possible. This section defines some basic
translations that partially capture some of these relationships:
- cooccurrence of variables
- The graph of the cooccurrence of variables is
defined as a graph,
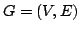 , with
, with 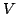 as the set of vertices that directly
correspond to the set of variables in the SAT instance, and
as the set of vertices that directly
correspond to the set of variables in the SAT instance, and 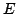 as the set of edges
defined as follows: for each clause
as the set of edges
defined as follows: for each clause 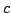 in the SAT instance if
in the SAT instance if 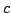 contains the variable
contains the variable
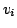 and the variable
and the variable  then there is an edge from the vertex
then there is an edge from the vertex 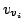 to vertex
to vertex
 .
.
- cooccurrence of literals
- The graph of the cooccurrence of literals is defined
as a graph,
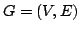 , with
, with 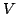 as the set of vertices that directly correspond to the
set of literals in the SAT instance, and
as the set of vertices that directly correspond to the
set of literals in the SAT instance, and 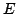 as the set of edges defined as
follows: for each clause
as the set of edges defined as
follows: for each clause 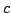 in the SAT instance if
in the SAT instance if 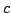 contains the literal
contains the literal 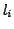 and
the literal
and
the literal 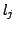 then there is an edge from the vertex
then there is an edge from the vertex 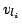 to vertex
to vertex 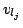 .
.
- simple implicational relations
- The graph of simple
implicational relations is defined as a graph,
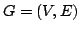 , with
, with 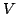 as the set of
vertices that directly correspond to the set of literals in the SAT instance, and
as the set of
vertices that directly correspond to the set of literals in the SAT instance, and
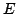 as the set of edges defined as follows: each clause
as the set of edges defined as follows: each clause
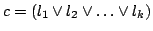 in the SAT instance is interpreted as an implicational statement
in the SAT instance is interpreted as an implicational statement
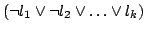 and there are directed edges from the
vertex
and there are directed edges from the
vertex  to
to
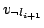 for
for 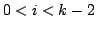 (when
(when 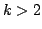 ) and the
directed edge
) and the
directed edge
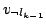 to
to 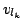 (when
(when 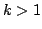 ). Note that the edges are
defined in the input order of the literals in a clause.
). Note that the edges are
defined in the input order of the literals in a clause.
- all possible implicational relations
- The graph of all possible implicational
relations is equivalent to the basic version, but instead of generating a linear
number of edges based on the the input order it generates edges for every possible
implicational relation that arises from each clause. For a clause of size
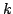 there are
there are
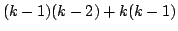 edges. A SAT instances with many large clauses means the resulting
graph size may be too large to adequately visualise.
edges. A SAT instances with many large clauses means the resulting
graph size may be too large to adequately visualise.


Next: Generating The Images
Up: Translating SAT Instances to
Previous: Translating SAT Instances to
Last modified: 2004-03-17
Andrew Slater