
Faculty of Engineering
and Information Technology
Department of Engineering
 |
Faculty of Engineering
and Information Technology
Department of Engineering
|
|
Nonlinear H-Infinity Control Singular information state dynamics
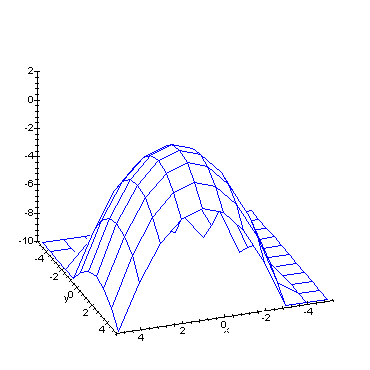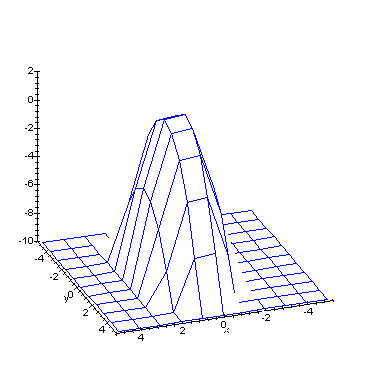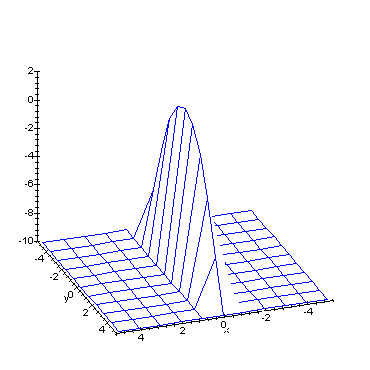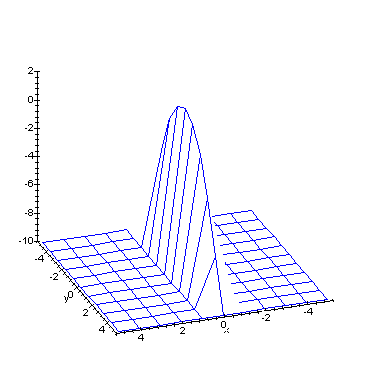
In this animated image we see the information state evolving as a function of time. You will notice that it collapses onto a vertical plane as time progresses, illustrating convergence to the singular equilibrium information state 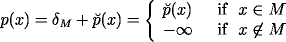
|
|||||||||||||||||||||||||||
| Page last updated: 6 March, 2007 Please direct all enquiries to: Matthew.James at anu.edu.au Page authorised by: Dean, FEIT |
| The Australian National University — CRICOS Provider Number 00120C |