Look anywhere in a circuit, the output of an antenna, a receiver, on the power supply lines .. and you will always see white noise. Often white noise is modelled as additive white Gaussian noise. AWGN noise is noise for which the probably of the ocurrence of an amplitude n(t) at time t follows a Gaussian distribution. The special significance of this is that the accumulated noise from a set of arbitrary noise sources will approach a Gaussian noise distribution for a large number of sources. This fact is referred to as the central limit theorem. Having sais this most noise in man made and is not therefore even Gaussian

White noise is generated by a body at finite temperature. The average power is given by,

where K_B is Boltzmann's constant (1.38x10^-23 J/^oK), T is the temperature in Kelvin and B the bandwidth in Hz. For example the noise power generated by a circuit component at room temperature (300 K) in a 200 kHz bandwidth is 8.28 x 10 ^-16 Watts = -120.8 dBm ( 1 mW = 0 dBm). Noise is fundamental and can only be reduced by cooling: hence the liquid helium cooled receivers used in radio-astronomy.

Conceptually the body referred to above is any body at all. If the body happens to be a resistor then the R.M.S. noise voltage developed across its terminals is V² = K_BTBR.

When noise is added to a signal and the spectra of the noise and signal overlap, then little can be done to uncorrupt the signal. The signal power to additive noise power ratio is the signal to noise ratio (SNR). When a signal of SNR, SNRi, with noise Ni is input to an active network like an amplifier and exits with a new SNR, SNRo with noise power No then we define the noise factor (F) of the network as,

From this we define the noise figure (NF) of the network as,

where A_v is the gain of the network. The meaning of this formula is that though strictly the noise is not amplified by the amplifier, more often than not, it is worse than if amplified. The NF compares the actual SNR at the output of the amplifier to what it would be if the amplifier actually amplified the noise but did not add to it. If the amplified input noise is equal to the noise at the output then we obtain a NF of 0 dB which is the best we can do. The higher the NF the worse is the network.

What about a lossy network? Explain why the NF of a network which only has attenuation (ie contains passive components like resistors and capacitors..no active devices), has a NF numerically equal to its attenuation in dB. HINT Does the noise depend on the value of a resistance? The problem is to explain why the noise is not attenuated like signal.

Most often the NF of cascaded active networks (amplifiers with gain) will depend most heavily on the NF of the first amplifier in the chain. This is because the noise at its output will be amplified with the signal through succeeding stages. As a result, the total noise factor F_TOT of a circuit chain is given by

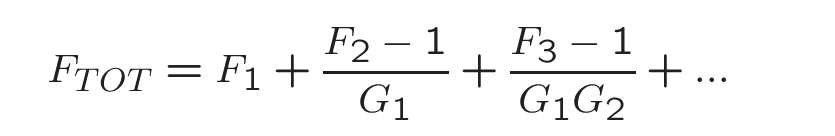
where F_k are the noise factors of the amplifiers and passive networks in the chain and G_k their gains or insertion losses.

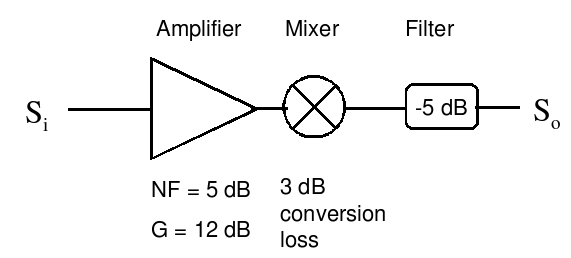
Ex. 21 Consider the following circuit. It consists of an amplifier, a mixer and a filter. The mixer and the filter are passive circuits with losses of 3 and 5 dB respectively. Assume that the receiver has a NF of 5 dB, a temperature of 0 celsius, and a standard noise power due to its internal resistances in a 1200 kHz BW.

(c) Repeat (b) for a temperature of -270 celsius.

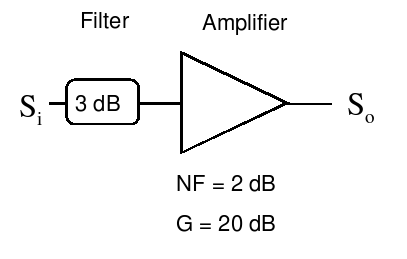
Ex. 22 Compute the NF for the following circuit

We close this section with a short word about a limitation that random noise imposes on the ability to transmit information. The SNR imposes a fundamental limit to the number of bits per second that can be trasnmitted over a communications link. Shannon's rule states that,

where B is the band width and SNR is the signal to noise ratio. If the SNR = 1, then C = B. Because the noise power, N = S_NB where S_N is the noise Power Spectral Density (P.S.D), the SNR approaches 0 as B approaches infinity. This implies that C approaches 1.443 S/S_N where S is the signal power. Alternatively we can write C = 1.443 B SNR = 1.443 B S/N.

Ex. 23 If the SNR on a telephone line is 30 dB (typically), what is the capacity given an equalised bandwidth of 3 kHz? How does this compare with 56 kbps? Explain this.