The estimation of the pose of the head is a basic functionality of visual face trackers and has been investigated by many researchers. In most systems the pose estimation is done in the next layer above the feature tracking layer. In our system there is a 2-D layer located in between hardware feature tracking and 3-D pose estimation. As stated in the previous section this layer has the purpose of increasing robustness by detecting and recovering from tracking errors.
Two different transformations may be used for pose estimation from monocular data: perspective or affine transformation. The perspective transformation precisely models the actual projection of a 3-D scene to the image plane. However, the required calculations are complex and time consuming and can deliver up to a fourfold ambiguity in the pose estimation. Perspective transformations are only used in systems running off-line in combination with the computationally expensive least squares model fitting. Real-time systems usually use affine transformation because it has simpler calculations and only a twofold ambiguity. This so called weak perspective is a parallel projection without depth forthshortening. It is a good approximation of perspective projection as long as the depth of the object does not exceed 1/10th of the distance between camera and object which is usually the case in face tracking applications.
Most pose estimations are based on the well-known three point model fitting algorithms proposed by Huttenlocher and Ullman or by Grimson, Huttenlocher and Alter. Least-square fitting algorithms are too slow, the selection of the three best tracking points causes unreliability in near frontal view situations and relying on simple heuristics such as the side of the image the centre of the feature set is within restricts the head translations to a minimum. We decided to choose to use the interference of the angle sets of multiple triplets to solve the twofold ambiguity of pose.


The figure above shows a typical tracking situation where the head is rotated slightly to the side, in this case about 15 degrees. The two triplets 1 and 2 are located in two different planes which intersect at an angle of 45 degrees. The local results of the inverse affine projection algorithm are the angles between the plane and the optical axis of the camera. The corresponding head rotational angles are calculated easily. Interference shows that only one head rotational angle satisfies the solutions for both triplets.
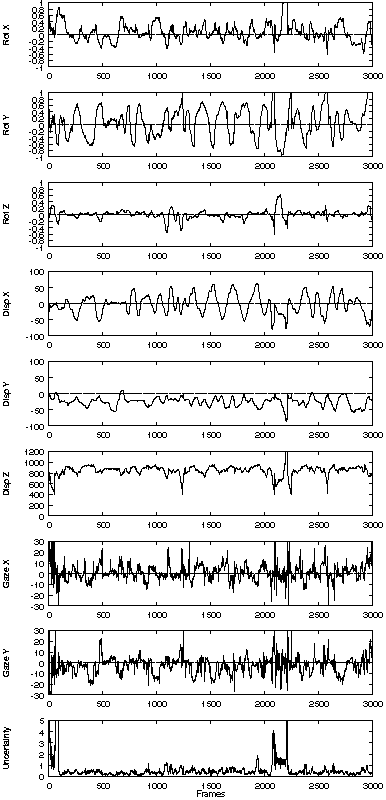
The following diagram shows the result from a pose estimation test sequence.