Using the Tableau Editor Help

The tableau editor is a tool which helps you to create semantic tableaux of the kind found in these notes. It does not construct tableaux for you—you have to decide which inferences to make and provide the details—but it does check your tableau step by step as you build it, and it gives you feedback on any errors. This is many times more efficient than handing in solutions to exercises and reacting to feedback from a lecturer or tutor: for one thing, the time between work and feedback is on the order of milliseconds rather than hours, days or weeks; for another, the comments are always accurate and never judgmental. The tool is always available and infinitely patient. Finally, it runs in your own browser, not on a web server anywhere else, and it keeps no record of your activity, so privacy is not an issue.

Using the tableau editor is fairly straightforward, if you have read the notes on semantics and have at least tried inventing tableaux and writing them out on paper. The menus and other controls are not especially complicated, but it is still worth reading through this short guide at least to clarify the details. As usual, the best way to learn is to practice, so try it for yourself and come back to this guide as a reference document.

Starting the tableau editor

The tableau editor starts automatically when you link to it. Point any browser at
html://users.cecs.anu.edu.au/~jks/LogicNotes/tableau_editor.html
You will be prompted to enter a problem to be solved, unless one was already specified as part of the URL, as happens when you follow a link to the tool from inside the Logic Notes.

Defining a problem

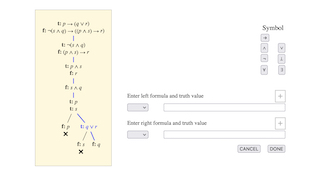
If you see boxes with a message that starts "Define the problem", you are being asked to specify the formulae to be analysed. If you want to test a sequent for validity, type the first premise in its box (see Typing a formula below). Choose "true" from the drop-down menu to the left. Repeat for each premise, using the "+" button to go to the next one. Then click "+" again and type the conclusion formula in its box, and set its truth value to "false". When the entire problem has been specified, click "DONE" and the top of the tableau will appear in the tableau display. You are then ready to begin constructing the tableau.

Selecting a branch

Initially, all the formulae are in one column, so the tableau has only the one branch. Later, after some splitting rules have been applied, there may be several branches. To proceed with building the tableau you must select a branch (even initially when there is only one). Do this by clicking just below the bottom formula in the branch. When the branch is selected, the lines running through it are highlighted in blue, as are any formulae which still need analysis. If the branch contains a contradiction (a formula with both labels "t" and "f") a cross will appear to show that the branch is closed and the contradiction will show up in red. If there is no contradiction and all formulae in the branch are fully analysed, the tableau can be regarded as finished and a message to that effect will appear. Otherwise, the action menu will appear and you can proceed. Re-clicking at the end of a selected branch de-selects it.

The usual action is to add to the tableau by analysing one of the formulae highlighted in blue. Decide which formula you want to analyse, and choose either to extend the branch or to split it according to the relevant rule for developing tableaux. Other actions are possible: see below.

Extending a branch

Most of the rules for developing formulae do not split the branch but merely add one or more signed formulae to the end of it. If there is a formula highlighted in blue whose development will be of this kind, you may choose "extend branch" from the action menu. You will be prompted to enter a formula by typing in the text box and its truth value by selecting from the small menu to its left. If you need to add two formulae (for instance, if you are developing a true conjunction by adding its two true conjuncts) click the "+" box and enter the second formula in the same manner. When everything is ready, click "DONE" to proceed. If all is well, your branch extension will be added to the tableau.

Splitting a branch

Some rules, such as the one for developing a true disjunction, split the branch into left and right sub-branches, adding formulae to each side. If there is a formula highlighted in blue whose development will be of this kind, you may choose "split branch" from the action menu. You will be prompted to enter formulae as in the case of extending the branch, but this time both left and right formulae must be entered. It does not matter which you specify as "left" and which as "right", but they must both be there and must both be completed before you click "DONE".

Backtracking

Developing a true existential formula or a false universal one involves extending the branch with an instance obtained by substituting a term for the variable. A term which already occurs in the branch may be used for this purpose, but it is not a typical instance of the quantified formula, so if it leads to a closed branch, that shows (almost) nothing. In such a case, you may backtrack on the choice of instantiator and try another term. If necessary, try using a name which does not occur in the branch; if that leads to closure, then the branch is dead. When you opt to backtrack, you are invited to choose the formula you want to change—it must be one of the purple-coloured ones—and the current branch will be unwound to the point where that formula was introduced. Extend with a different instance and carry on.

Other formulae, including all propositional formulae, are not backtrackable, so backtracking only applies in special circumstances when building tableaux for quantified logic.

Typing a formula

Text may be typed or copy-pasted into the long text area when extending or splitting a line. Letters such as 'p' or 'F' are typed as normal, as are parentheses and the identity symbol '='. Symbols for connectives or quantifiers may be selected by clicking the appropriate buttons. They may also be input as text using the same conventions as Logic for Fun. That is, you may type 'AND', 'OR', 'NOT', 'IMP', 'IFF', 'BAD', 'ALL' and 'SOME' in place of 'AND', 'OR', 'NOT', 'IMP', 'IFF', 'BAD', 'ALL' and 'SOME'. Note these have to be in upper case. Hitting the 'Return' or 'Enter' key causes the formula to be parsed, so that can optionally be used to check syntax, but nothing else happens until "DONE" is clicked.

Generally, parentheses are required around any sub-formula with a binary main operator (including '='). If they are omitted, association to the left will be assumed unless a preference to the contrary has been set. Unary operators (including 'NOT' and quantifiers) have minimal scope, so if they are applied to a sub-formula with a binary main operator, parentheses will be required. Function and predicate symbols, variables and names are all single letters, so they may be written as a sequence without spaces or as a comma-separated list in parentheses. That is, 'Pafab' is the same as 'Paf(a,b)' and also the same as 'P(a,f(a,b))'. Use whatever variant of the notation you find most convenient.

Letters have specific uses:

a…e		names (individual constants);
f…h		function symbols;
F…H		monadic predicate symbols;
p…t		propositional (sentential) atoms;
P…T		relation symbols;
v…z		variables.

Attempting to use a letter for the wrong purpose (e.g. using x as a propositional atom or a as a variable) is a syntax error. Any letter may be followed by zero or more primes, giving a, a′, a′′, etc, so the supply of symbols is unlimited.

Note that a monadic predicate symbol is a kind of relation symbol, and a propositional atom is also a kind of relation symbol (just a zero-adic one) so you can use P as a monadic predicate or indeed as an atom if you wish, without violating the restrictions on uses of letters. Similarly, you can use f as a constant, because a name is in principle just a 0-adic function symbol, but confusing yourself by torturing the notation is not recommended!

The tableau display

The tableau under construction is displayed in the main yellow box. It begins at the top with the formulae defining the problem, and grows downwards as formulae are developed in branches. Developing a formula in one branch has no effect in any other branch. If a branch has been selected, it is highlighted and some formulae in it may be shown in blue, red or dark violet to indicate that they need development, are part of a contradiction or result from backtrackable decisions respectively.

Since these are labelled tableaux, each formula has a label saying whether it is true or false. The rule for developing a formula depends on its truth value (its label) and on its main operator. One effect of this is that every formula in the tableau is (up to substitution of terms for variables in the quantified case) a subformula of one of the initial formulae.

Not every formula requires explicit development. If the results of developing it are already in the branch, it counts as fully analysed. For instance, if t: p is already in the branch for some other reason, there is no need to apply any rule to t: p OR q, so it will not be highlighted when the branch is selected.

The action menu

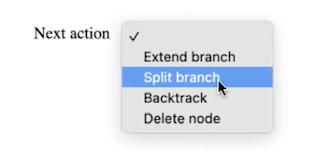
When a branch is selected and contains formulae which still require development, the action menu appears. Use it to choose whether to extend or split the branch, or to undo previous actions.

There are four available actions:

Extend branch: One or two formulae with their truth values may be added to the currently selected branch. They will then appear in the tableau below a short vertical line.
Split branch: The current branch will be divided into two continuations. One formula is added in each, except where a biconditional is developed, in which case two formulae are added in each continuation. The newly added formulae will appear in the tableau joined to the branch by oblique lines.
Backtrack: Return to an earlier point in the branch where a true existential or false universal was instantiated with a previously used term. You will be prompted to choose the backtrack point by clicking on it. If there is no backtrackable decision in the current branch, backtracking is not possible.
Delete node: Undo the last 'extend' or 'split' action in the currently selected branch. If this was a split, the other side of the split will be removed as well, even if there is a tree of formulae below it.

Error messages

As each formula is added, it is checked for syntactic well-formedness and each branch extension or split is checked to see that it does indeed develop some formula from the branch. If any error is detected, a message appears in a a box at the bottom of the window. To proceed when you get an error message, do as it says and select from the menu to the right.

Before doing that, it is important to make sure you understated what the tableau editor is complaining about: why is it an error? If it isn't obvious, the first thing to try is usually to click on the formula you were trying to develop. That will result in a more informative error message. In case it still isn't clear, the 'Help' option points to a page of the glossary which may serve as a starting point.

The usual response to an error message is to edit the formulae and truth values you are currently adding. To do this, take the first menu option, "Continue". Do not try to change the input without choosing from the menu, as it won't work. You also have the option to go further back and clear all the boxes in order to re-start the extension or split. More radically, you can choose to skip out of the current action altogether and return to the stage of choosing an action. If you then want to go right back to choosing a branch, just click on the currently selected one to de-select it.

The error messages are quite brief, and sometimes a bit technical (as you would expect, given that they come from checking the technicalities) but they are intended to be helpful rather than critical. We all make mistakes sometimes and so we all see these messages; the key is to make constructive use of them.