[ENGN3213 Home]

Canonical Forms

There are two standard or canonical  ways of expressing boolean functions:

1.

Sum-of-products (SOP).  E.g.

$$X = A + \overline{B}C + \overline{A}BC$$

2.

Product-of-sums (POS)   E.g.

$$X = (A+D)(C+\overline{D})(\overline{B}+C)$$

These representations are useful for

• direct implementation, and
• starting logic function minimization.

We will focus on SOP.

Consider

$$f(A,B,C) = A + \overline{B}C + \overline{A}BC$$

where

• product terms A, $\overline{B}C$, $\overline{A}BC$  
• minterms $\overline{A}BC$  

A minterm is any ANDed term containing all of the varibles (perhaps complemented).

Let's look at the truth table which corresponds to this function:

	A	B	C	f(A,B,C)
m0	0	0	0	0
m1	0	0	1	1
m2	0	1	0	0
m3	0	1	1	1
m4	1	0	0	1
m5	1	0	1	1
m6	1	1	0	1
m7	1	1	1	1

(Check this!)

Each row of the truth table corresponds to one of the 2ⁿ = 8 possible minterms in n=3 variables.

$$m_i = m_i(A,B,C), \ \ i=0, \ldots, 2^3-1$$

E.g.

$$m_3 = \overline{A}BC = 001$$

Actually, the truth table specifies the function as a sum of minterms:

$$\begin{array}{rl} f(A,B,C) & = m_1 + m_3 +m_4 +m_5 + m_6 + m_7 \\ & = \sum m(1,3,4,5,6,7) \end{array}$$

This is called the canonical SOP representation   of the function f.

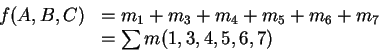
The minterm code   for n=3 is as follows:

m0	0	0	0	$\overline{A}$	$\overline{B}$	$\overline{C}$
m1	0	0	1	$\overline{A}$	$\overline{B}$	C
m2	0	1	0	$\overline{A}$	B	$\overline{C}$
m3	0	1	1	$\overline{A}$	B	C
m4	1	0	0	A	$\overline{B}$	$\overline{C}$
m5	1	0	1	A	$\overline{B}$	C
m6	1	1	0	A	B	$\overline{C}$
m7	1	1	1	A	B	C

Complemented variables correspond to 0 and uncomplemented variables correspond to 1.

The function $f(A,B,C) = A + \overline{B}C + \overline{A}BC$ can be put into canonical SOP form algebraically as follows:

$$\overline{B}C = (\overline{A}+A) \overline{B}C = \overline{A} . \overline{B}C +A \overline{B}C = m_1 + m_5$$

$$A = (B + \overline{B})A = \ldots = m_4 + m_5 + m_6 + m_7$$

(fill in the missing steps!) and so on combining we get $f(A,B,C) = \sum(1,3,4,5,6,7)$ as before.

Any Boolean function can be expressed in canonical SOP form.

[ENGN3213 Home]