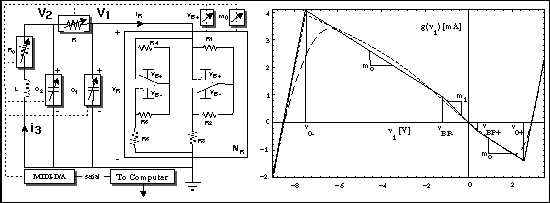
Chua's circuit is a third-order electrical circuit built from an inductor, two capacitors, several (linear) resistors, and a nonlinear resistor NR. The circuit and the nonlinear conductance characteristic of NR is shown below.

The nonlinear resistor is built using resistors and two opamps, giving rise to the piecewise-linear conductance characteristic (this depends on saturation of the opamps for large enough voltages).

Here is a pspice schematic:

Chua's circuit has three ``equilibria'' (linear circuits only have one equilibrium), and depending on the values of the components, the circuit can exhibit a whole range of nonlinear behaviour such as

• bifurication
• asymptotic stability to an equilbrium
• asymptotic stability to a limit cycle (stable periodic motion)
• multiple-period oscillation
• Chaos :
• Spiral Chua strange attractor
• Double-scroll Chua strange attractor

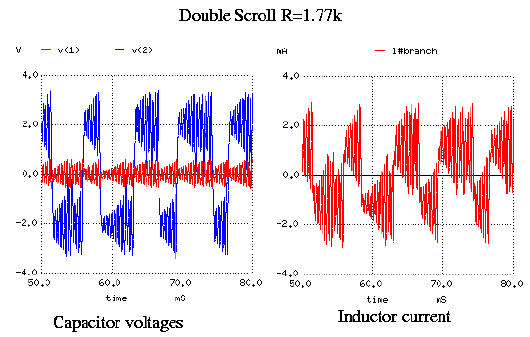
Here are waveforms for the two capacitor voltages and the inductor current in the case
R=1.77k, corresponding to the double-scroll Chua attractor:

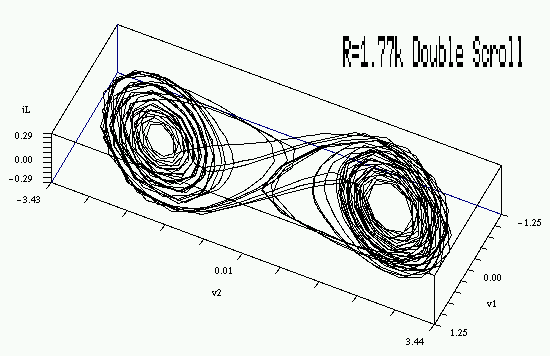
Notice the erratic nature of the waveforms. This is illustrated in the next picture which shows a plot of the waveforms in the 3-d space with coordinates (v1,v2,iL) - each point on the curve corresponds to voltage and current values at an instant in time, so the curve represents a path parameterized by time.

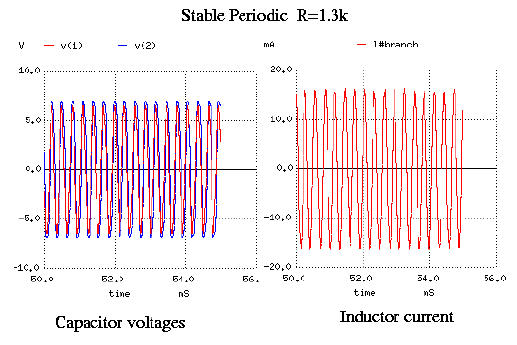
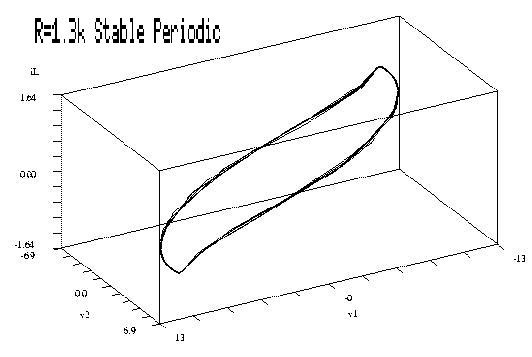
The waveforms are completely different if we set R=1.3k. The waveforms are now regular, predictable, and periodic:

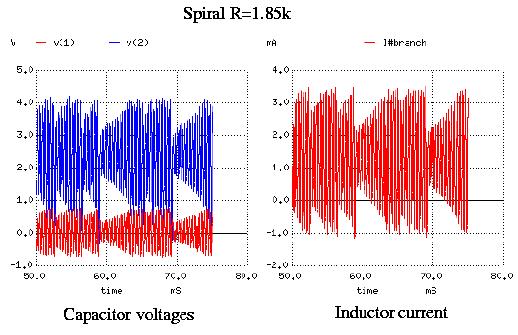
Another important case of interest is the spiral attractor, for R=1.85k.

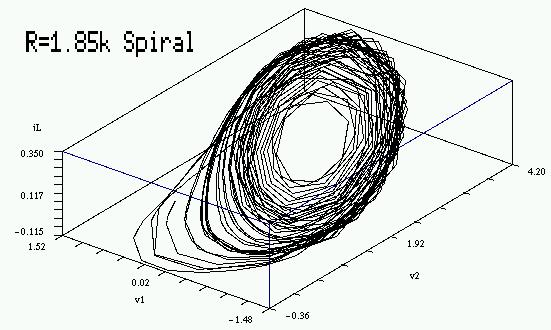
You can investigate Chua's circuit using the spice file chua.sch

When experimenting with Chua's circuit, keep all the component values fixed except for the 2k potentiometer which you can adjust to see the different behaviours. Have a look at the waveforms produced by the capacitor voltages.

References:

1. M.P. Kennedy, ``Three Steps to Chaos - Part II: A Chua's Circuit Primer'', IEEE Trans. Circuits and Systems - 1: Fundamental Theory and Applications, Vol. 40, No. 10, Oct. 1993, 657-674. (A detailed technical paper on the Chua circuit and its behaviour.)
2. http://www.ccsr.uiuc.edu/People/gmk/Papers/ChuaSndRef.html (Making sounds from Chua circuits.)
3. J. Gleick, ``Chaos: Making a New Science'', Viking Penguin, New York, 1987. (A popular account of nonlinear dynamics.)

Last updated: February 25, 1999 / Matt James