Data sheets for both FET and Bipolar Junction RF power transistors carry two essential pieces of information for RF power circuit design. These are the large-signal equivalent input and output impedances and the output power obtainable as a function of input power. The large signal input and output impedances could either be in series or parallel form but using the the relations for these interms of circuit Q, it is easy to convert. Take a look at Figures 2-8 and Figure 15 of the MRF134 data. These parameters are for high power design and would have quite different values in the small signal case. Notice that the S-parameters are also available in Table 1. These are only relevant for small signal operation and should only be used for a first attempt at a high power design. By now we are good at this.

Often the resistive part of the output impedance is not given. For example, if one looks at page 2 of the MRF134 data, only the capacitances are listed. These capacitances have the same meaning as they did for the bipolar transistor and do allow an RF equivalent circuit to be developed. For high power design we assume that the load resistance that we require is that which gives our desired power for the maximum possible excursion of the output voltage VIZ R_L = (V_DS - V_sat)²/(2P). We therefore must include a matching network to make that tunes out the capacitance of the output stage and makes the load impedance (Z₀ if connecting to a transmission line) equal to this value.

Example

Since the design of RF transistor amplifers involves no new concepts, we go through the design of the 150 MHz test circuit in the MRF134 data sheet.

Consider the input circuit in Figure 1. We can summarise it as follows.



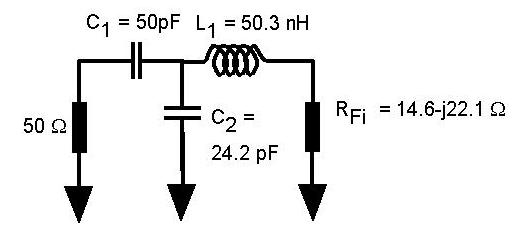
The 68 Ohm will be ignored in the following because it says in Figure 15 of the data sheet that it was included in the measurement of the input FET impedance = 14.6 - j22 Ohm. In doing this design we don't know in advance what Q the design engineer had chosen. However the circuit indicates considerable variability in component values to allow for variations in the transistor parameters. By assuming C₁ = 50 pF, we can start the calculation. In retrospect we'll see that a Q of about 2 was intended. Of course in doing our own designs we would pick Q first!

Using the technique described in the chapter on matching, we recognise the matching circuit as a T-network. We therefore include a virtual resistor as shown in the following.



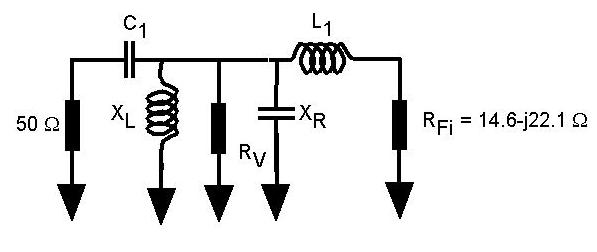
Note that capacitor C₂ has been split into an L in the left circuit and a C in the right circuit because of their respective requirements for the achievement of a complex conjugate. Since R_v is in a parallel combination (in both the left and the right circuits), its value must be greater than the R_S = 50 Ohm (source resistance) or R_Fi = 14.6 Ohm the FET input resistance. According to our recipe for determining Q the larger Q would be given by Q = Q_R = (R_v/R_Fi - 1)^1/2, where the R subscript refers to the right circuit. Similarly Q_L = (R_v/R_S - 1)^1/2.

Consider the left circuit. Since we know C₁ with X₁ = 21.2 Ohm at 150 MHz, Q_L = X₁/R_S = 0.424. We obtain R_v = R_S(1 + .424²) = 59 Ohm. The part of C₂ (which is an inductor in the left circuit) is given by R_v/X_2L = .424 => X_2L = 139Ohm.

Consider the right circuit. From the above expression for Q we obtain Q_R = (R_v/R_Fi - 1)^1/2 = (59/14.6 - 1)^1/2 = 1.74. The part of C₂ (which is a capacitor in the right circuit: To be checked ) is given by R_v/X_2R = 1.74 => X_2R = 33.3 Ohm. The combined reactance of L₂ and the reactance of the FET, call it X_1R' = Q_RR_Fi = 1.74*14.6 = 25.4 Ohm. Thus L₁ = (25.4 + 22.1)/(2p150MHz) = 50.3 nH.

Thus we are justified in using a capacitor for C₂. If we wish to replace the left and right shunt elements by a single capacitor then we combine the j139Ohm and the -j33.3Ohm in parallel, which corresponds to C₂ = 24.2 pF for operation at 150 MHz.

This completes the design of the input circuit.

The output circuit looks as follows.



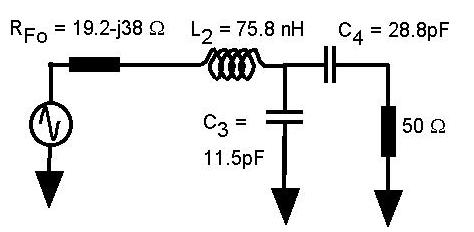
The procedure is similar to that for the input circuit. Here however we may as well assume a Q of 1.74 so that the input and output Q's are at least matched. In the case of the output circuit, we are transforming from the output of the transistor to the 50 Ohm load, but this makes no difference. The virtual resistor is given by R_v = R_Fo(1 + Q²) = 77.3 Ohm where R_Fo = 19.2 Ohm is the FET output resistance. The final values obtained are L₂ = 75.8 nH, C₃ = 11.5 pF and C₄ = 28.8 pF. Once again we have chosen to lump the left and right circuit shunt reactances into C₃ as required.

The inductor dimensions are given in the Caption for Figure 1. Using the formula for inductance with N = 3, r = .394cm and l = .51 cm for L₁ in the input circuit and N = 3.5, r = .394 cm and l = .635 cm for L2 in the output circuit, we obtain, L₁ = 63.7 nH and L₂ = 75.7 nH.

You may try the following...

• Redo the above design for a 60 MHz amplifier. Assume Z_in = 28.6 - 29j and Z_out = 20.5 - 58.1j at 60 MHz.