
INITIALIZE
1
2 NIL
3 for all
4 do
5 NIL
RELAX
1 if
2 then
3
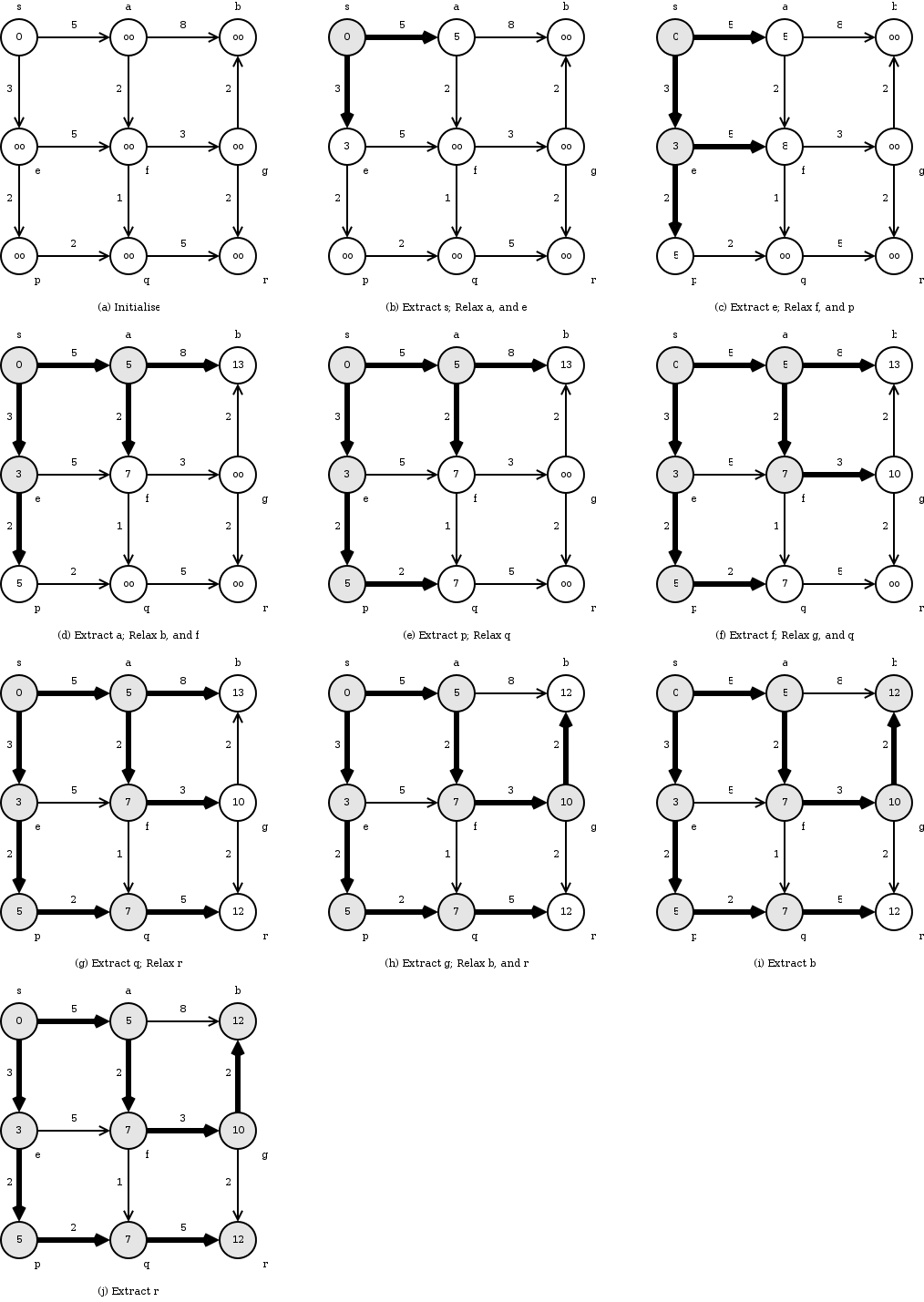
DIJKSTRA-SHORT
1 INITIALIZE
2
3
4 while
5 do EXTRACT-MIN
6
7 for each vertex
8 do RELAX
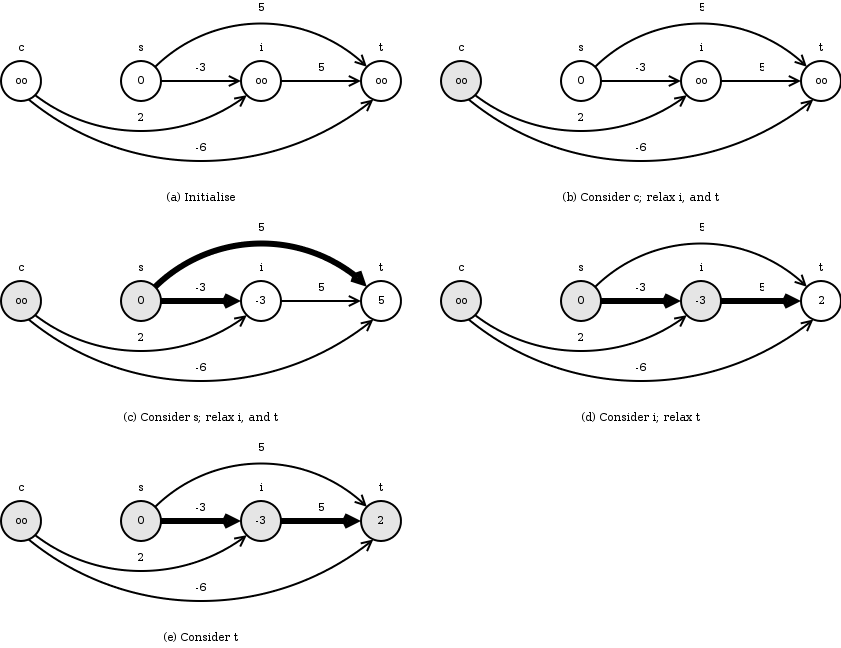
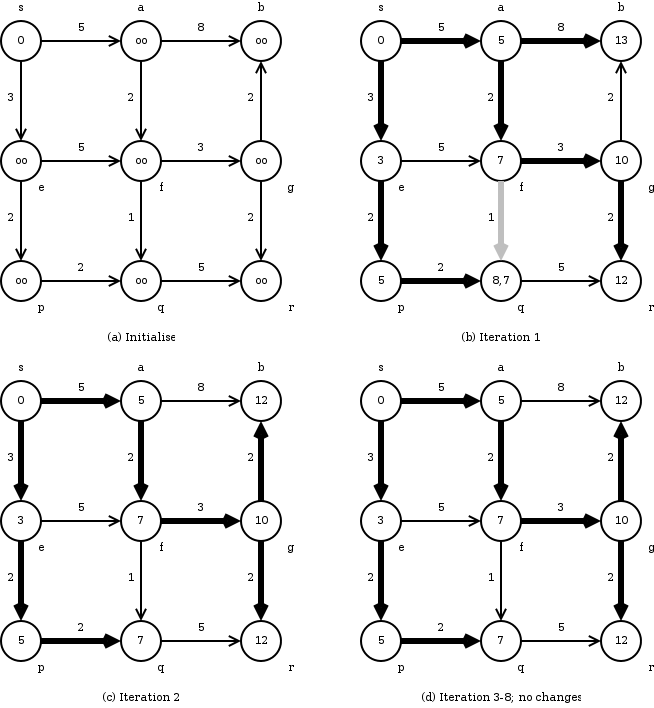
BELLMAN-FORD
1 INITIALIZE
2 for to
3 do for each edge
4 do RELAX
5 for each edge
6 do if
7 then return FALSE
8 return TRUE
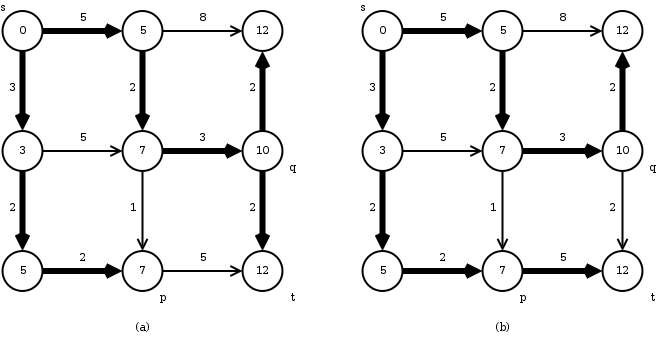
DAG-SHORTESTFigure 5 shows an example execution of DAG-SHORTEST on a DAG.
1 Topologically sort the vertices of
2 INITIALIZE
3 for each vertex taken in topologically sorted (increasing) order
4 do for
5 do RELAX