




BFS
1 for each vertex
2 do WHITE
3
4 NIL
5 GRAY
6
7 NIL
8 /* Q always contains the set of GRAY vertices */
9 while
10 do
11 for each
12 do if
13 then GRAY
14
15
16 ENQUEUE
17 DEQUEUE
18 BLACK
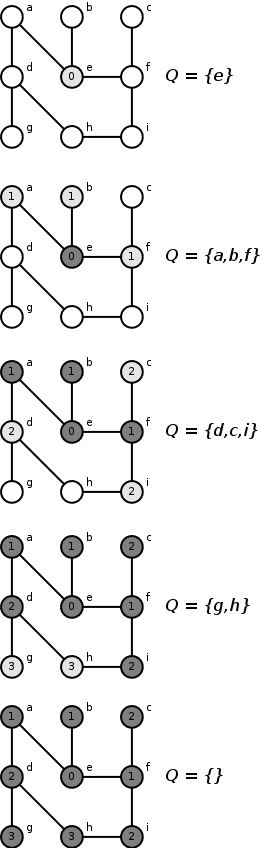
DFS
1 for each vertex
2 do WHITE
3 NIL
4
5 for each
6 do if
7 then DFS-VISIT
DFS-VISITConsider the following undirected graph. In DFS, all vertices are initialised to WHITE, then each one is visited if they are white. Assuming that , DFS-VISIT is first invoked on . Within DFS-VISIT, is coloured GRAY, then the vertices adjacent to are visited recursively if they are WHITE. When all visits are completed, is coloured BLACK (note that DFS still works if we leave it as GRAY). This results in the visiting order .
1 GRAY
2
3
4 for each
5 do if
6 then
7 DFS-VISIT
8 BLACK
9
10




STRONGLY-CONNECTED-COMPONENTSThe running time of the algorithm is . Steps 1 and 3 take time. Step 2 requires time, and Step 4 takes time. Thus, the algorithm takes time.
1 finish-order finish order of DFS( )
2 transpose of
3 dfs-forest DFS trees from DFS( )
. visited in reverse finish-order.
4 return dfs-forest
. /* each tree in dfs-forest is a strongly connected component. */