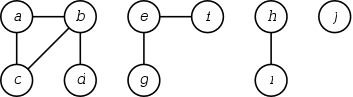
CONNECTED-COMPONENTS
1 for each
2 do MAKE-SET
3 for every edge
4 do if FIND-SET FIND-SET
5 then UNION
SAME-COMPONENTS
1 if FIND-SET FIND-SET
2 then return TRUE
3 return FALSE

| Edge processed | Collection of disjoint sets | |||||||||
| initial sets | ||||||||||
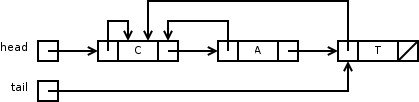
MAKE-SET ,What's the total time complexity of the above operations? A weighted-union heuristic: Assume that the representative of each set maintains the number of objects in the set, and always merge the smaller list to the larger list, then Theorem: Using the linked list representation of disjoint sets and the weighted-union heuristic, a sequence of MAKE-SET, Union, and Find_Set operations, of which are MAKE-SET, takes time. Hint: observe that for any , after 's representative pointer has been updated times, the resulting set containing must have at least members.
MAKE-SET ,
,
MAKE-SET ,
MAKE-SET ,
UNION ,
UNION ,
,
UNION .
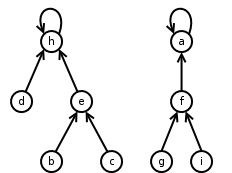

MAKE-SET
1
2
FIND-SET
1 if
2 then FIND-SET
3 return
UNION
1 LINK( FIND-SET , FIND-SET )
LINKwhere is the height of in the tree. If both of the above methods are used together, the time complexity is . The Rank properties
1 if
2 then
3 else
4 if
5 then