Hash Tables

Hash tables associate keys with values. It is a generalization of the simple array of values. Directly addressing into an ordinary array makes effective use of our ability to examine an arbitrary position in an array in

O (1)

time. Hash tables support the the following operations:

SEARCH( $table, key$ ) $\to$ $value$
INSERT( $table, key, value$ )
DELETE( $table, key$ )

The simplest technique of implementing a dynamic set that supports the directory operations is direct addressing. In direct addressing, every possible key maps to a unique position in the table. Conversely, each position in the table maps to a unique key. Direct addressing only works if no two elements share the same key. For this reason, the approach works well when the universe,

U

, of keys is reasonably small. This is because we need one table slot for each key in

U

, hence if

| U |

is large, our memory requirements will be large. Direct address operations on a table

T [0 \dots m - 1]

with

m

slots are defined as follows:

DIRECT-ADDRESS-SEARCH $(T, k)$
1 return $T [k]$

DIRECT-ADDRESS-INSERT $(T, k, x)$
1 $T [k]$ $\leftarrow$ $x$

DIRECT-ADDRESS-DELETE $(T, k)$
1 $T [k]$ $\leftarrow$ NIL

When

U

is large, and

K

, the set of all the actual keys, is small, a lot of space is wasted in direct addressing. In many applications,

U

is very large relative to

K

. An example is a database index. If we are indexing a 32-bit integer column, we will need one slot for each possible integer, in the case of 32-bit, that's over 4 billion slots! Even in a large database, with one million rows, we are still only using 0.025% of our table to index that column. Furthermore, each integer in that column has to be unique in order for the direct address table to work. A solution to this is using hash tables.

1 Hash tables

Whereas direct addressing stores is each element with

k

in slot

k

, in a hash table, a function,

h

, is used to work out which slot

k

should be stored in. That is, each element with key

k

is stored in slot

h (k)

h

maps the universe

U

of keys into the slots of a hash table

T [0 \dots m - 1]

h (k) \to {0, 1, \dots, m - 1}, where k \in U

We say that an element with key

k

hashes to slot

h (k)

, we also say that

h (k)

is the hash value of key

k

1.1 Collision in Hash tables

Because the number of keys in

U

may be greater than

m

, more than one key may be mapped by

h

onto the same slot. For the INSERT operation, if the slot is empty, then there is no problem. However, if the slot is already occupied, by a prior insertion of another key that hashed into the same slot, then a collision has occurred.

One effective way to solve the collision is so called resolution by chaining. In this method we use a linked list at every position in the hash table to store keys. Hence, if a key is hashed to the same value as a previous key when inserting, the new key is simply added to the head of the linked list. When searching, the key is first hashed, and then a search is done on the corresponding linked list.

Figure 1: A chained hash table. Each slot points to a linked list, empty slots and the end of the lists are in grey.

The directory operations on a hash table

T

are easy to implement when collisions are resolved by chaining.

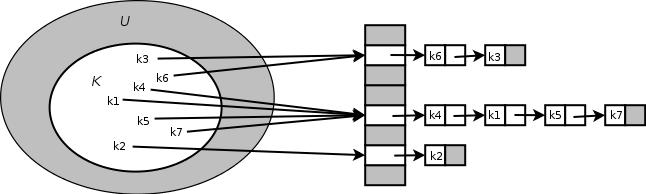
CHAINED-HASH-SEARCH $(T, k)$
1 Search for an element with key $k$ in list $T [h (k)]$

CHAINED-HASH-INSERT $(T, x)$
1 Insert $x$ at the head of list $T [h (key [x])]$

CHAINED-HASH-DELETE $(T, x)$
1 Delete $x$ from the list $T [h (key [x])]$

1.2 Analysis of hashing with chaining

The load factor,

α

, of a hash table is defined by the number of elements in the table,

n

, over the number of slots

m

α = \frac{n}{m}

The worst case behaviour for searching for an element in the table is where every element hashes to the same value. In that case, the time is

O (n)

. However, the average case is much better, at

Θ (1 + α)

Theorem: In a hash table in which collisions are resolved by chaining, an unsuccessful search (or a successful search) takes time $Θ (1 + α)$ under the assumption of simple uniform hashing - all elements are equally likely to hash into any slot, independently of where any other element has been hashed into.

2 Designing hash functions

A good has function satisfies the assumption of simple uniform hashing: each key is equally likely to hash to any of the

m

slots, independently of where any other key has hashed to. This section examines the following three hash function schemes that assume that the universe of keys is the set

N = {0, 1, 2, \dots}

of natural numbers.

Hashing by division
Hashing by multiplication
Universal hashing

2.1 The division method

The division method involves mapping

k

into the

i

th slot where

i

is the remainder when

k

is divided by the number of slots,

m

. That is, the hash function is:

h (k) = k \mod m

For example, if

m = 23

and the key

k = 107

, then

h (k) = 15

2.2 The multiplication method

The multiplication method for creating hash functions operates in two steps.

Multiply the key $k$ by a constant $A$ in the range $0 < A < 1$ and extract the fractional part of $kA$ .
Multiply this value by $m$ and take the floor of the result.

In short the hash function is:

h (k) = ⌊ m (kA \mod 1) ⌋

where $kA \mod 1$ means the fractional part of

kA

, that is,

kA - ⌊ kA ⌋

For example, if

m = 10000

k = 123456

and

A = \frac{\sqrt{5} - 1}{2} = 0.618033

, then

\begin{matrix} h (k) & = & ⌊ 10000 \times (123456 \times 0.61803 . . . mod 1) ⌋ \\ = & ⌊ 10000 \times (76300.0041151 . . . mod 1) ⌋ \\ = & ⌊ 10000 \times 0.0041151 . . . ⌋ \\ = & ⌊ 41.151 . . . ⌋ \\ = & 41 \end{matrix}

The advantage of this method is that the value of

m

is not critical.

2.3 Universal hashing

If a malicious adversary chooses the keys to be hashed, then he can choose

n

keys that all hash to the same slot, yielding an average retrieval time of

Θ (n)

. Any fixed hash function is vulnerable to this sort of worst case behaviour. The only effective way to improve the situation is to choose the hash function randomly in a way that is independent of the keys that are actually going to be stored. This approach is called Universal Hashing.

The main idea of universal hashing is to select the hash function at random at run time from a carefully designed class of functions.

Let

H = {h_{1}, h_{2}, \dots, h_{l}}

be a finite collection of hash functions that map a given universe

U

of keys into a range

{0, 1, \dots, m - 1}

. Such a collection is said to be universal if for each pair of distinct keys

x, y \in U

, the number of hash functions

h \in H

for which

h (x) = h (y)

is precisely

\frac{| H |}{m} = \frac{l}{m}

3 Open Addressing

One of the disadvantages of chained hashing is that we need to have enough space to store

m

pointers in the hash table,

n

elements, plus a further

n

pointers for the linked lists from each element.

In open addressing, rather than needing a pointer for each element, the elements are stored in the hash table itself. Thus the space requirements are constant, at enough space to store

m

elements.

To make open addressing work, we successively probe the hash table until we find an empty slot in which to put the key. The sequence of positions probed depends on the key being inserted. To determine which slots to probe, we extend the hash function to include the probe number as a second input. Thus, the hash function becomes

h : U \times {0, 1, \dots, m - 1}, \to {0, 1, \dots, m - 1}

With open addressing, for each

k

, the probe sequence

(h (k, 0), h (k, 1), \dots, h (k, m - 1))

is a permutation of

{0, 1, \dots, m - 1}

so that every hash table position is eventually considered as a slot for a new key as the table fills up.

HASH-INSERT $(T, k)$
1     $i$ $\leftarrow$ $0$
2    repeat $j$ $\leftarrow$ $h (k, i)$
3                     if $T [j] = NIL$
4                           then $T [j]$ $\leftarrow$ $k$
5                                       return $j$
6                           else   $i$ $\leftarrow$ $i + 1$
7    until $i = m$
8    error "Hash table overflow."

HASH-SEARCH $(T, k)$
1     $i$ $\leftarrow$ $0$
2    repeat $j$ $\leftarrow$ $h (k, i)$
3                     if $T [j] = k$
4                           then return $j$
5                      $i$ $\leftarrow$ $i + 1$
6    until $T [j] = NIL$ or $i = m$
7    return NIL

3.1 Linear Probing

Given an ordinary hash function

h' : U \to {0, 1, \dots, m - 1}

, the method of linear probing uses the hash function

h (k, i) = (h' (k) + i) \mod m

for

i = 0, 1 \dots, m - 1

. Given key

k

, the 1st slot is

T [h' (k)]

, the 2nd slot is

T [h' (k) + 1]

, and so on up to slot

T [m - 1]

. Then we wrap around to slots

T [0], T [1], \dots

until we finally probe slot

T [h' (k) - 1]

Figure 2: An example of linear probing. In this example, the keys

k_{1}, k_{2}, \dots, k_{6}

were inserted in that order respectively. The indicators on the right show where each key initially hashed to.

The disadvantage of linear probing is the primary clustering problem. This is where the table develops clusters of successive used slots, so finding values that are hashed to that area starts to move away from the performance of direct addressing. The above diagram shows a mild example primary clustering.

3.2 Quadratic Probing

Quadratic probing uses a hash function of the form

h (k, i) = (h' (k) + c_{1} i + c_{2} i^{2}) \mod m

where

h'

is an auxiliary hash function,

c_{1}

and

c_{2}

are constant.

This method works much better than linear probing, but to make full use of the hash table, the values

c_{1}

c_{2}

and

m

are constrained. Also, if two keys have the same initial probe position, then their probe sequences are the same since

h (k_{1}, 0) = h (k_{2}, 0)

implies

h (k_{1}, i) = h (k_{2}, i)

. This leads to the secondary clustering problem.

3.3 Double hashing

As seen with the two previous methods, clustering was always a problem. To avoid clustering, a more random like method is needed. This is found in double hashing. Double hashing uses a hash function of the form

H (k, i) = (h_{1} (k) + i h_{2} (k)) \mod m

where

h_{1}

and

h_{2}

are auxiliary hash functions. The initial position is

T [h_{1} (k)]

, from then on, successive positions are offset from the previous position by

h_{2} (k)

, module

m

Figure 3: An example of double hashing.

k_{5}

probes a different set of positions to

k_{2}

, hence a place is found quicker for it.

The value

h_{2} (k)

must be relatively prime to the hash table size

m

for the entire hash table to be searched. Otherwise,

m

and

h_{2} (k)

have greatest common divisor

d > 1

for some key

k

, then search for key

k

only examine

(1 / d)

th the hash table.

For example,

m

is a prime and

\begin{matrix} h_{1} (k) & = & k \mod m, \\ h_{2} (k) & = & 1 + (k \mod m') \end{matrix}

where

m'

is chosen to be slightly less than

m

(say

m - 1, m - 2

k = 123456

and

m = 701

, we have

h_{1} (k) = 80

and

h_{2} (k) = 257

Double hashing represents an improvement over linear or quadratic probing in that

Θ (m^{2})

probe sequences are used, rather than

Θ (m)

, since each possible

(h_{1} (k), h_{2} (k))

pair yields a distinct probe sequence, and as we vary the key, the initial probe position and the offset may vary independently.

File translated from T_EX by T_TM, version 3.67.
On 31 Mar 2006, 18:12.