Binary Heaps

A binary heap data structure is a binary tree that is completely filled on all levels, except possibly the lowest, which will be filled from the left up to a point. Due to these characteristics, it is easy to represent the tree in an array. Figure 1 shows the logical structure (top) of the heap and also how it can be stored in an array (bottom). Notice how each layer of the tree occupies consecutive slots in the array. The root of the tree is

A [1]

, and given the index

i

of a node, the indices of its parent PARENT

(i)

, left child LEFT

(i)

and right child RIGHT

(i)

can be computed simply.

PARENT $(i)$
1 return $⌊ i / 2 ⌋$

LEFT $(i)$
1 return $2 i$

RIGHT $(i)$
1 return $2 i + 1$

Binary heaps can either be a maximum heap or minimum heap. As a maximum heap, every node indexed by

i

, other than the root (i.e.

i \neq 1

), has

A [PARENT (i)] \geq A [i]

. Conversely in a minimum heap, every node indexed by

i

, other than the root, has

A [PARENT (i)] \leq A [i]

. The remainder of this lecture assumes a maximum heap.

Note: This property makes a binary heap different from a binary search tree. In a binary tree, $left child \leq parent < right child$ . However, in a maximum heap, $parent \geq left child$ and $parent \geq right child$ . So a binary search tree can be viewed as sorted, while a heap cannot.

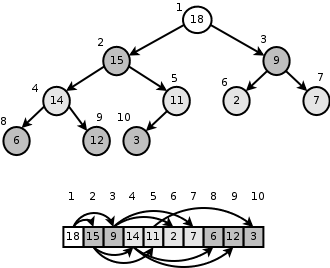Figure 1: The structure of a maximum heap. The top diagram shows the logical heap, the bottom diagram shows how it can be stored in an array, still showing the heap structure. Numbers in the circles/boxes are keys and those outside are indices. Notice how each layer of the tree occupies consecutive slots in the array.

1 Maintaining the heap property

Assuming that we already have a maximum heap, operations on a maximum heap, for example inserting or deleting, may cause the heap to lose its maximum heap property. The MAX-HEAPIFY routine can be used to rectify this. It takes an array

A

and index

i

, and assumes that

A

is a maximum heap except that

A [i]

may be less than its children.

MAX-HEAPIFY $(A, i)$
1     $l$ $\leftarrow$ LEFT $(i)$
2     $r$ $\leftarrow$ RIGHT $(i)$
3    if $l \leq heap-size [A]$ and $A [l] > A [i]$
4          then $largest$ $\leftarrow$ $l$
5          else   $largest$ $\leftarrow$ $i$
6    if $r \leq heap-size [A]$ and $A [r] > A [largest]$
7          then $largest$ $\leftarrow$ $r$
8    if $largest \neq i$
9          then Swap $A [i]$ and $A [largest]$
10                       MAX-HEAPIFY $(A, largest)$

Figure 2: In (a), 5 has been added to position 2 in a maximum heap. The first iteration of MAX-HEAPIFY swaps 5 with 14, in (b), and then swaps 5 with 12 in (c).

2 Building a heap

The BUILD-MAX-HEAP routine takes any array

A

, and, working successively from the bottom of tree to the top, uses MAX-HEAPIFY to build the maximum heap.

BUILD-MAX-HEAP $(A)$
1     $heap-size [A]$ $\leftarrow$ $length [A]$
2    for $i$ $\leftarrow$ $⌊ length [A] / 2 ⌋$ downto $1$
3             do MAX-HEAPIFY $(A, i)$

Figure 3: (a) The initial tree. BUILD-MAX-HEAP works successively from the bottom. 18 is greater than its children, so nothing is done. (b) MAX-HEAPIFY is called on 3, and so is swapped with 12. (c) 1 will be swapped with 8. (d) 2 will be sent to the bottom of the tree, first swapped with 18, then with 4. (e) When MAX-HEAPIFY is called on 5, it is sent to the bottom of tree. (f) The resulting maximum heap.

3 Priority Queues

A priority queue is a data structure for maintaining a set

S

of elements, each with an associated value called a key.

Priority queues are often used to efficiently extract an element with a particular property out of a dynamic set. They do this by maintaining the position of element in the set that holds that property, and keeping the rest of the set ordered in such a way that modifying the set will lead to easily finding the new element with the given property.

A max-priority queue supports the following operations.

INSERT ( $S, x$ ) inserts the element $x$ into the set $S$ ., i.e., $S \leftarrow S \cup {x}$ .
MAXIMUM( $S$ ) returns the element of $S$ with the largest key.
EXTRACT-MAX( $S$ ) removes and returns the element of $S$ with the largest key.
INCREASE-KEY( $S, x, k$ ) increases the value of element $x$ 's key to the new value $k$ , which is assumed to be at least as large as $x'$ s current key value.

A maximum heap can be used as a max-priority queue, as it always maintains that the first element is the maxmimum. Using MAX-HEAPIFY, it can easily ensure that certain changes, for example removing the maximum element, will maintain the first element as the maximum.

HEAP-MAXIMUM $(A)$
1 return $A [1]$

HEAP-EXTRACT-MAX $(A)$
1    if $heap-size [A] < 1$
2          then error "Heap underflow"
3     $max$ $\leftarrow$ $A [1]$
4     $A [1]$ $\leftarrow$ $A [heap-size [A]]$
5     $heap-size [A]$ $\leftarrow$ $heap-size [A] - 1$
6     MAX-HEAPIFY $(A, 1)$
7    return $max$

HEAP-SIFT-UP $(A, i)$
1    while $i > 1$ and $A [PARENT$ (i) $] < A [i]$
2                  do Swap $A [i]$ with $A [PARENT$ (i) $]$
3                         $i$ $\leftarrow$ PARENT $(i)$

HEAP-INCREASE-KEY $(A, i, k)$
1    if $k < A [i]$
2          then error "New key is smaller than current key"
3     $A [i]$ $\leftarrow$ $k$
4     HEAP-SIFT-UP $(A, i)$

MAX-HEAP-INSERT $(A, k)$
1     $heap-size [A]$ $\leftarrow$ $heap-size [A] + 1$
2     $A [heap-size [A]]$ $\leftarrow$ $k$
3     HEAP-SIFT-UP $(A, heap-size [A])$

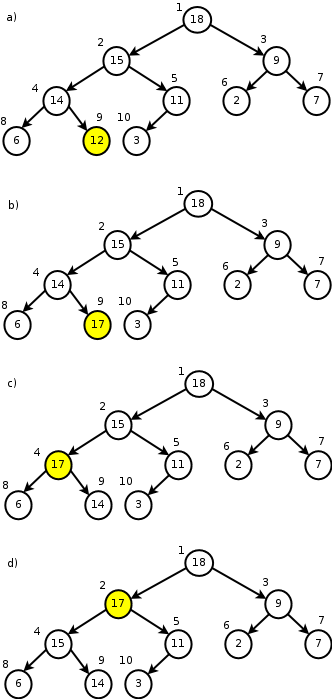Figure 4: HEAP-INCREASE-KEY (a) The original maximum heap with the key to be increased shaded in yellow. (b) The key is increased to 17. (c) 17 is swapped with its parent. (d) The maximum heap property is restored, swapping 17 with its parent again.

File translated from T_EX by T_TM, version 3.67.
On 31 Mar 2006, 18:12.