Growth of Functions
The analysis of algorithms often requires a body of mathematical
tools. In this lecture, we introduce some important tools and
standards of notation.
- Asymptotic notation
- Standard notation and common functions
1 Asymptotic Notation
The notation used to describe the asymptotic running time of an
algorithm is defined in terms of functions whose domains are the set
of natural numbers.
This notation refers to how the problem scales as the problem gets
larger. In some cases it is important to look at how fast the
problem is for small amounts of input, particularly when the same
task is being done over and over again. However, we are mainly
concerned with algorithms for large problems, hence how the
performance scales as the problem size approaches infinity is what
we will look at.
1.1
-notation
O-notation, pronounced "big-oh notation", is used to describe the
asymptotic upper bound of an algorithm. Formally, it is defined as:
For a given function,
, we denote by
the set of
functions,
{
: there exist positive constants
and
such that
for all
}.
Less formally, this means that for all sufficiently big
, the
running time (space requirements etc) of the algorithm is less than
multiplied by some constant. Even less formally, if
then we can say that
runs no slower than
.
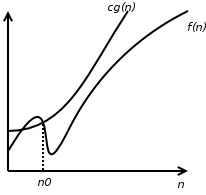 Figure 1: "There exist positive constants
and
such that
for all
."
is
thus
.
For example:
Figure 1: "There exist positive constants
and
such that
for all
."
is
thus
.
For example:
- Given
, then
.
- Given
, then
.
- Given
, then
.
1.2
-notation
-notation, pronounced "big-omega notation", is used to
describe the asymptotic lower bound of an algorithm. Formally, it
is defined as:
For a given function,
, we denote by
the set
of functions,
{
: there exist positive
constants
and
such that
for
all
}.
Less formally, this means that for all sufficiently big
, the running time (space requirements etc) of the algorithm is
greater than
multiplied by some constant. Even less
formally, if
then we can say that
runs
no faster than
.
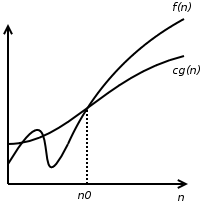 Figure 2: "There exist positive constants
and
such that
for all
."
is
thus
.
For example:
Figure 2: "There exist positive constants
and
such that
for all
."
is
thus
.
For example:
- Given
, then
.
- Given
, then
.
- Given
, then
.
1.3
-notation
We can now talk about algorithms in terms of a limit to how fast or
how slow they run. However, our notation is not
asymptotically tight. If we say that an algorithm runs in
, then that algorithm could actually run in
time. Usually we want to have a tight bound, we want to be able to
say that an algorithm runs no slower and no faster than a particular
function. To do this, we use
-notation.
For a given function,
, we denote by
the set
of functions
{
: there exist positive
constants
,
, and
such that
for all
}.
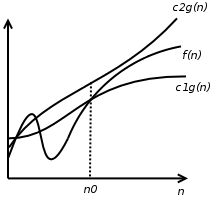 Figure 3: "There exist positive constants
,
, and
such that
for all
".
is thus
.
For example:
Figure 3: "There exist positive constants
,
, and
such that
for all
".
is thus
.
For example:
- Given
, then
.
- Given
, then
.
1.4
-notation
Sometimes we want to identify bounds that are not asymptotically
tight,
-notation, pronounced little-oh notation. is used to
denote an upper bound that is not asymptotically tight.
For a given function,
, we denote by
the set of
functions
{
: for any positive constant
, there exists a constant
such that
for all
}.
The implication of this, is that
becomes
insignificant relative to
as
approaches infinity:
For example,
but
.
1.5
-notation
-notation, pronounced little-omega notation, is used to
denote a lower bound that is not asymptotically tight.
For a given function,
, we denote by
the set
of functions
{
: for any positive
constant
, there exists a constant
such that
for all
}.
The implication of this is that
becomes
insignificant relative to
as
approaches infinity:
For example
but
.
File translated from
TEX
by
TTM,
version 3.67.
On 31 Mar 2006, 18:12.



